As promised, this is a follow-up to one of the summary posts from the FQXi conference in Vieques. If you have read those, you may recall that Anthony Aguirre asked the intriguing question: is there any way for us to tell if the universe is infinite or simply really, really big? (George Musser has also blogged about this.) In this blog post I suggest one possible way in which this might be accomplished. I emphasize that much of the content of this post is entirely speculative but it does offer suggestions on how to more rigorously determine the validity of the conjecture. It relies, however, on an assumption that runs entirely counter to my own conclusion in my most recent FQXi essay: that bits (in some fashion) constitute the basic building blocks of the universe.
The Setup
Consider the following string of binary digits
...011010010101101...
where, for the moment, we assume that the full string is infinite but that we only have knowledge of the sub-string shown above. Now consider the following maps:
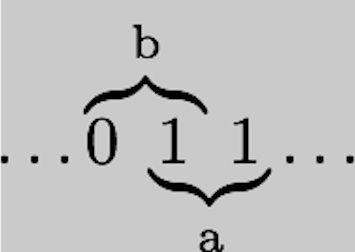
00 --> a
11 --> a
01 --> b
10 --> b
Notice that each digit in the original string ends up getting counted twice.
Thus the original string can be mapped to
...XbabbbabbbbabbY...
where the X and the Y are unknown given that we do not know what precedes the 0 on the left and what follows the 1 on the right. Formally, this second string is doubly-infinite meaning its cardinality is double the cardinality of the first string since every digit in the first string is counted twice (yes, there are actually levels of infinity!).
Now suppose that we have complete knowledge of the doubly-infinite string of a's and b's with the exception of one value. It should be relatively clear that, if we know the distribution of 0's and 1's in the original string (e.g. 60/40 or 30/70), then the unknown value in the second string should be immediately known unless the original distribution is 50/50 in which case we have no idea (try it!).
So now take any two locations, X and Y, on what we call the "image" string (the strings of a's and b's) with the caveat that there are at least two letters between them. Suppose that we have complete knowledge of the doubly-infinite string other than these two locations. From the argument in the preceding paragraph, it should be clear that the instant we know one of these two values (say X), we immediately know the other (Y). A formal proof of this appears in Section 5 of this article by Steve Shea, which is open access.
Do we really need an infinite amount of knowledge?
The way I have described the problem (courtesy of Steve Shea) would seem to imply that we need to know absolutely every value in the doubly-infinite string, i.e. we need an infinite amount of knowledge, if we are to correctly predict the value of Y given the value of X (which also assumes that the original string of 0's and 1's is not a 50/50 split). But this gets to the heart of Anthony's problem: do we really need an infinite amount of knowledge or just a whole lot of knowledge? One could imagine that we could approach a very high probability of correctly predicting Y given our knowledge of X as our knowledge of the doubly-infinite string gets large (though I would like to emphasize that I am not aware of a formal proof of this as yet--Steve's article has just been published, though he's been working on it for several years).
Nevertheless, approaching such a high-degree of accuracy with a prediction would also seem to require that the strings really are infinite. One can imagine that if they are not infinite, there could be some sort of "edge" effect caused by the fact that the second string would be ill-defined at the ends and that such an effect could somehow propagate through the string (again, I emphasize that this is speculation at this point and that there is no formal proof of this). For example, we could interpret the mapping (and thus, to some extent, the original string) as being nothing more than a kind of production rule somewhat akin to those in formal language theories: it's just a rule for generating the string of a's and b's (note that in such theories the "start" symbol need not be at the extreme left or right of a string which means it could still be infinite--if you are unfamiliar with the concept of a "start" symbol, a good read is Douglas Hofstadter's Pulitzer Prize-winning opus Gödel, Escher, Bach). Given that (and assuming that the ratio of 0's to 1's in the original string is not unity, i.e. they are not a 50/50 split since, otherwise, there really is no production rule), it should be clear that the a's and b's are interdependent which means I could rewrite the production rule simply in terms of the a's and b's themselves. Inherent in the original rule, however, there is no way to deal with endpoints. Specifically, the endpoints of the string of a's and b's would be ill-defined based on the production rule which would make any neighboring values in the string undefined and so on such that the entire string is ill-defined (e.g. it would be as if there was no "start" symbol). Thus the string must be infinite, at least in this formal system.
I would then conjecture that while the strings themselves must be infinite, we only need a finite (though arguably large) amount of knowledge in order to predict Y given X with a high degree of accuracy. Of course this all hinges on whether or not the original string is completely random. If the original string of 0's and 1's is exactly 50/50, the value of Y cannot be predicted with any greater accuracy than 50% (which essentially means it cannot be predicted at all). Likewise, the requirement that the string of a's and b's be infinite no longer holds, i.e. it's really a relic of the production rule.

A universe of qubits
What does any of this have to do with the universe? Let's just suppose that John Wheeler was correct and that, at its core, the universe is built up from bits--binary digits--or, rather, qubits. Since we don't actually see the world as 0's and 1's (or answers to yes/no questions) it is clear that there is some form of mapping that goes on at some deep level from these binary questions to something slightly less fundamental. Let's take, as a first approximation, the map introduced at the beginning and suppose that the string of a's and b's represents the results of measurements of simple two-level quantum systems. In other words, the a's and b's represent our knowledge of the universe at its most fundamental level (notice that it may or may not suggest a deeper reality of 0's and 1's or even something else entirely). We might then imagine that the universe (or, rather, our knowledge of it) can be reduced to a sub-string of a very, very long (possibly infinite) string of outcomes of measurements on qubits. This is not so radical an idea, by the way (see Seth Lloyd's article on this topic: arXiv:1312.4455).
One glitch in this argument, of course, is that we don't know the order of the measurement outcomes, i.e. the string of a's and b's. We have small strings of correlated outcomes, but we don't know for certain if all of these small strings are part of one larger string, i.e. if we know, for example,
...abbababa...
...babbabab...
...aaababaa...
is it necessarily true that
...abbababa...babbabab...aaababaa...
or that
...babbabab...abbababa...aaababaa...?
If all of the sub-strings indeed are part of one, larger string it would seem to suggest that all possible qubit measurements in the universe may be correlated in some way since, as long as there exists a production rule, we can connect even the most far-flung elements of the full string of a's and b's. This, also, is not such a radical idea if we take the correlations as being equivalent to quantum entanglement (see Buniy and Hsu's article on this: arXiv:1205.1584v2).
Note that there is one question here that I have not addressed and that is whether knowledge of X necessarily implies that Y is the opposite of X. If the a's and b's represent measurement outcomes for entangled qubits then one would seem to expect that the outcomes of X and Y must be opposite one another. There is no requirement in the mathematics that this be the case. In addition the mathematics imply a string of somewhat looser correlations (recall they must be at least two letters apart) in between the entangled pair. It might be possible to address the latter through something like quantum teleportation, but I won't address that here. Instead I will simply assume that the production rule is such that the sub-strings that are accessible to us appear to behave in such a way that X and Y always behave as if they are entangled.
Is the universe infinite or just really, really large?
Let's take Buniy and Hsu's idea as correct in which case all qubit measurements are somehow part of a single, large string. We can access different sub-strings of this larger string via entanglement measurements. Note, however, that X and Y do not necessarily need to be in the same sub-string. So, for instance, an entanglement experiment with qubits might represent the following pair of sub-strings
...abbabaXabbaba...ababaabYbabaaba...
In other words, we are ignorant of some of the intermediary processes that connect them. Nevertheless, we do know that a determination of X immediately tells us what Y must be since this is measurable in a laboratory. This suggests that the intermediary processes, while perhaps not readily apparent to us, nevertheless exist as long as there is a production rule and as long as the full string is doubly-infinite. In fact, if Buniy and Hsu are correct (and note that their argument is based on cosmological models and thus not dependent on anything I suggest here), the mere presence of entanglement suggests that the string of all qubit measurements in the universe is infinite which would itself suggest that the universe is infinite, but only if the underlying production rule is not completely random. Recall that none of this works if the 0's and 1's in the original string are a 50/50 split. If they are, there is no correlation between X and Y.
I caution against rushing to judgement about these ideas. Clearly we see correlations and entanglement in the universe on some level. Does this automatically imply, then, that the universe is infinite and not entirely random at its base level? It clearly does not since we don't know if Buniy and Hsu are correct. In other words, we have no idea of our measurements of entanglement are merely parts of one large, interconnected string of such measurements. What it does seem to tell us is that if they are correct (and it is a big "if"), then it is highly likely that the universe is both infinite and non-random. (It also would seem to suggest that Max Tegmark might be right after all about the role mathematics plays in the universe.)
Now Anthony was interested in this from the standpoint of the multiverse and one could easily modify these ideas to take that into account. I won't do it here. I can also imagine someone taking Steve's results without reference to Buniy and Hsu and coming up with a way to measure whether the universe is infinite or merely very large.
There are a lot of assumptions and conjectures in this post but there are also a lot of concrete starting points for further exploration. Can we definitively prove, mathematically, that these strings must be infinite for this effect to be possible? I offered a heuristic argument above as to why, but a more formal proof would be welcome. Can we really re-interpret Steve's original mapping in a way that makes it self-referential to the string of a's and b's, i.e. can we find a production rule for the string of a's and b's such that it would exactly match what we would have obtained using the original mapping? Conversely, if we can't, can we definitively rule out the possibility that one exists? Are Buniy and Hsu correct in suggesting that all particles in the universe are ultimately entangled and can we actually reduce everything to a set of qubit measurements? What might the results presented here say about the multiverse? Is there some other way to work with these results that might say something useful about the size of the universe?
In my mind, these are all ideas worth pursuing and so I suppose you could interpret this blog post as a challenge: let's get some answers to these questions!