Quantum entanglement is the great soap opera of modern physics. The human spectacle--Einstein discovers entanglement, his colleagues mostly ignore him--was bad enough. But the particles themselves are enacting a sappy romance. Bring two of them together (they also do threesomes and more) and they establish a bond that no physicist can put asunder, acing the particulate equivalent of the Newlywed Game, in which physicists make measurements on the particles and the particles respond in a coordinated way.聽
But how do they do that? What *is* entanglement, really? Is there any explanation for it or must we accept it as a brute fact of the world? These are the questions that have brought me to the National University of Singapore's Centre for Quantum Technologies (CQT), which is graciously hosting me for two months so I can get away from the hurly-burly of my day job at Scientific American and start work on a book. (An FQXi mini-grant is also helping to cover my expenses.) I had been here hardly more than a few days before faculty member Valerio Scarani and his colleagues posted a paper (arxiv.org/abs/1110.3795) on precisely the questions that motivated my trip.
Their research concerns one of the possible ways entangled particles might stay in sync: they pass hidden signals between them. Theory and experiment rule out standard lines of communication such as light rays, so these hidden signals would have to be an exotic backchannel like nothing else in nature. They are strictly private to the entangled particles; a third party such as a latter-day Alexander Graham Bell can't commandeer the backchannel to transmit his or her own messages.
Experiments using closely synchronized measurements on entangled particles have shown hidden signals would need to zap from one particle to the other at least 10,000 times faster than light. (See also "The Speed of Spookiness" by CQT's Vlatko Vedral.) So, any such backchannel would flout Einstein's special theory of relativity. But that's not a deal-breaker. As long as the signals are hidden, they pose no overt contradiction to relativity. Besides, it's not as though physicists have a lot of other good options to explain entanglement. Once-promising possibilities, such as some internal memory to the particles, have been ruled out.
A hidden signal 10,000 times faster than light would be practically instantaneous, but for theorists, "practically" instantaneous is a long way from truly instantaneous. No matter how high the speed is, as long as it is finite, they can think of entanglement as a process that unfolds in spacetime. It starts at particle A and covers the distance to particle B. But if the speed is truly infinite, then the very concept of a propagating signal makes no sense. Once at A, it is automatically at B, too.
No direct timing experiment could ever tell whether the speed were truly infinite; a lower limit is the best it can do. But Scarani and his co-authors--Jean-Daniel Bancal, Antonio Acin, Yeong-Cherng Liang, and FQXi members Stefano Pironio and Nicolas Gisin--have found an indirect, though no less powerful, way to gauge the speed of putative hidden signals.
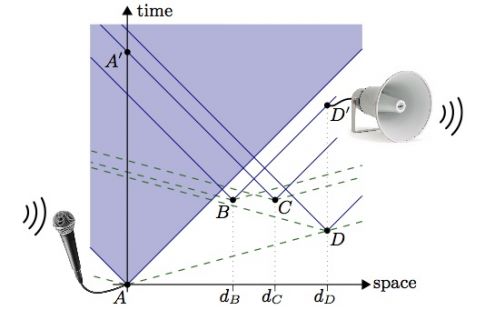
An earlier paper by Scarani and Gisin outlined the basic argument. Suppose you have three entangled particles interconnected by hidden faster-than-light signals. You measure both particles A and B at exactly the same time--too quickly for the hidden signal to pass between them--so the outcomes should be uncorrelated. A short while later, you measure particle C. A hidden signal *does* have time to get to it from the other particles, so C will be correlated with both of them. But if A and C, and B and C, are correlated, then surely A and B should be, too. Ergo, a contradiction--in which case hidden signals can't have a finite speed after all.
arXiv:1110.3795v1
This argument has a loophole, though. Just because A and C, and B and C, are correlated doesn't necessarily mean that A and B are, too. In fact, there are counter-examples in which they're not. The new paper gets around that by bringing in a fourth entangled particle. Then the argument does hold. Two of the particles are measured at precisely the same moment; the outcomes are uncorrelated. But the correlations among the other particles imply that those two particles should be correlated after all. "You really cannot construct an explanation of quantum mechanics with signaling," Scarani says. "The speed must be infinite, full stop."
(Image above right courtesy of Bancal et al.)
The authors quantify this conclusion in terms of an inequality. Finite-speed hidden signals would satisfy the inequality, but quantum mechanics violates it. In fact, in quantum mechanics, such signals could never remain hidden. Third parties would be able to exploit them, in overt contradiction with relativity theory. All good relativity-loving physicists must conclude that, to remain hidden, the bonds between entangled particles would have to act in a truly instantaneous way.
If so, whatever causes entanglement does not travel from one place to the other; the category of "place" simply isn't meaningful to it. It might be said to lie *beyond* spacetime. Two particles that are half a world apart are, in some deeper sense, right on top of each other. If some level of reality underlies quantum mechanics, that level must be non-spatial. The prime example of a theory that postulates such a reality, pilot-wave theory, is holistic--bound together into an inseparable whole, allowing effects to appear instantaneously in every corner of space. (For more on pilot-wave theory, see "Teaching an Old Wave New Tricks" (pdf).) Maybe that should please the lovers of the world. On the quantum level, they really are inseparable.
I am grateful to Theiss Research, under whose auspices I received an FQXi mini-grant to help pay my way in Singapore.
(Edited on 26 October to clarify what all good relativity-loving physicists must conclude, in response to Ken Wharton's comment.)