The aim of the recent FQXi conference on the nature of time was to explore time from a multidisciplinary, multifaceted viewpoint. As such the conference brought together psychologists, neuroscientists, complexity theorists, evolutionary biologists, journalists and science writers, as well as the usual cadre of physicists, philosophers, and the odd mathematician or two. Personally I thought it was a rousing success. Of course one of the drawbacks of bringing together such a broad group of researchers is that the way each communicates within their particular discipline. Each field has its own specialized jargon and notation, sometimes conflicting with the jargon and notation of other fields. One of the most glaring examples of this is the notation used by mathematicians and physicists when describing the behavior of operators and their matrix representations. Mathematicians (and sometimes mathematical physicists) use an asterisk to denote the adjoint (complex conjugate transpose) of an operator. Physicists, on the other hand, use a dagger. This gets confusing because the physicists use the asterisk to denote just the plain old complex conjugate (no transpose!). It gets even more confusing when you realize that the mathematicians use an overbar for the complex conjugate while the physicists use the overbar to indicate a vector which can be acted on by an operator! Is your head spinning yet?
At any rate, while it is safe to say we all were able to communicate reasonably well across disciplinary barriers at the conference, there were occasional points of confusion. With that said, a deep commonality emerged from across the spectrum of talks and discussions. First, it seemed quite clear that complexity, in some form or another, was at the heart of nearly every discussion. In other words, regardless of whether we are talking about multiple universes or electric fish, time has something to do with complexity. Second, it also seemed fairly clear that entropy is ultimately a measure of complexity. Thus the second law of thermodynamics seems to tell us that, roughly, complexity (and thus entropy) tend to increase in the long run and this is where the "arrow of time" seems to come from. The disagreements arose largely from our rather fluid understanding of complexity, entropy, and the second law.
So just what is entropy? Operationally it appears to be some type of measurable quantity (we'll get to exactly what that means in a moment) that tends to increase, on average, for the universe as a whole. In fact, the second law of thermodynamics specifically says that the entropy of any isolated system never decreases (on average) over time. Most people would assume that the universe is the ultimate isolated system - unless, of course, one believes in the multiverse. As such it seems that entropy is a thermodynamic quantity - and here's where the trouble starts.
From the standpoint of pure thermodynamics, i.e. macroscopic arguments, entropy can be related to internal energy, pressure, volume, temperature, chemical potential, and a host of other thermodynamic quantities via what are known as thermodynamic identities. Thus we often feel justified in associating entropy with energy (note that there are other reasons, but this is just one example). This association is the source of one problem that was discussed extensively at the conference: why is the entropy of the early universe low? More importantly, how is it that the state of the early universe contains high-energy particles but has low entropy and then evolves to a state in which the particles are low-energy but have a high entropy?
There are several answers to these questions and I won't endeavor to present them all. But I will present two. The first potential answer is that there isn't actually a problem here at all: all that energy in the early universe is (slowly) being used to increase its entropy. In this case entropy doesn't increase of its own accord (spontaneously) - energy must be injected into the system in order for the entropy to increase. The second potential answer is that maybe, just maybe, entropy has nothing to do with energy. Sure, they relate in some equations such as the thermodynamic identities, but that doesn't necessarily mean they are universally interdependent.
To expand on this it is necessary to actually give a definition to entropy. Now entropy is a concept that turns out to be fairly universal. It pops up in many different guises and forms including information theory. In fact one interpretation of entropy is that it is information.
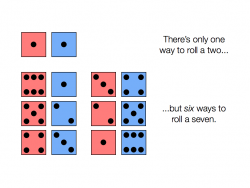
In statistical mechanics (the microscopic way of looking at thermal systems) and a few other fields, entropy is often interpreted as a logarithmic scaling of the number of possible configurations that a system could have. So, for example, one could define the "entropy" for a pair of dice as essentially counting how many ways one can get a certain number. Thus the "entropy" of a roll of seven would be higher than the "entropy" of a roll of two since there's only one way to get a two on a pair of dice but six ways to get a seven.
What does that have to do with the universe? Well, think of it this way. The very early universe (but post-inflation, so roughly 10-32 seconds after the Big Bang) consisted of a quark-gluon plasma. There are only a few possible processes at this point and so there's not much you can do with all those quarks and gluons. I mean, you might think there's a completely clean slate and anything is possible, right? But there really isn't. For example, until the so-called "quark epoch" between 10-12 and 10-6 seconds after the Big Bang, particles don't have any mass. By acquiring mass, the universe adds a little bit of variety to the mix. Think of it like this: the quark-gluon plasma prior to the action of the Higgs mechanism would be like having a box full of square, two-by-two Legos of only two colors. You can certainly build a lot with that, but good luck making a model of Princess Leia in Jabba the Hutt's lair. Adding mass is like adding, say, another color or shape to the Legos in your box - you can now do a little more with them. The variety is a bit greater.
So while it is true that, generally speaking, the universe contains the same amount of mass-energy now as it did then, it currently comes in a wider range of fundamental building blocks than it did in the beginning. So it makes sense that the current entropy of the universe is greater than it was. What about the entropy of the universe trillions of years from now? Currently the most accepted model of the universe's evolution has it expanding forever (thanks to the acceleration of its expansion) which should eventually produce a universe of nothing but individual fundamental particles of low-energy that aren't bound to anything and tend to be spatially isolated from one another. How could that state have a higher entropy than the current one?
Think about the Legos again. The current state of the universe is a bit like having a box full of a wide variety of Legos but with most of them already put together to form buildings, people, etc. In other words, you can do more with a box full of unused Legos than you can with a bunch of Legos that are already being used in some model: when you buy a new set of Legos, the entropy of the set is at its highest before you actually build the model because at that point those Legos could be used to build anything!
So if we view entropy in this manner, it is not in the least bit surprising that the early universe has a low entropy (despite consisting of high energy particles) while the much later universe will have a considerably higher entropy (despite consisting of low-energy particles). We could then view the Second Law of Thermodynamics as representative of the universe's desire (or, perhaps, the desire of the stuff in the universe) to be in the state that offers the greatest possible number of configurations, i.e. the state that maximizes the variety of possibilities. One could alternately say that the universe tends towards a state of increasing complexity.
If one looks closely at many of the talks from the conference (available on YouTube) one will find that most have some relation to complexity or statistical arguments (though sometimes not in an obvious way). In fact just about every talk at the conference touched on one or more of the following topics: quantum mechanics, statistical mechanics, probability & statistics, and complex systems. So it's fairly safe to say that if you want to understand what time is (and it's clear that we still don't), those are the topics you would do well to study.
With that said, I will close with some thoughts shared in casual conversation by Julian Barbour. As Julian says, if you want to properly define time you need to first answer the question: what is a clock? But in order to answer that question, you need answer this one: just what is duration anyway? Can entropy help answer that? It's an open but intriguing question. It means a lot of us will be busy thinking about this stuff for awhile.