Recently I attended the "New Directions in the Foundations of Physics" organized under the guidance of FQXi member Jeffrey Bub. In a series of blog posts I will present the main new ideas, and today I want to start with a talk by Adan Cabello which fired my, and everyone else's, imagination: "(Non-) Contextuality of Physical Theories as an Axiom."
To set the stage, let's go back in time to the proof of the Kochen-Specker theorem. What Kochen and Specker showed was that for some quantum systems one cannot pre-assign values for all possible measurement outcomes. For example, a spin one system has the following property called the 1-1-0 rule: measure the spin-squared on any 3 mutually orthogonal directions and you will always find the answers to be two ones and one zero on the three directions. Now it is possible, for example, to find a set of 33 directions on a sphere in such a way that all 3 orthogonal directions respect the 1-1-0 rule. In fact this has become a child's game of coloring 33 x 2 dots with say one green (corresponding to a zero) and two reds (corresponding to a one) for all orthogonal three sets of directions. In the end it cannot be done consistently.
聽
What this means is that in quantum mechanics the results of the experiments are "contextual": they depend on the measurement context and they cannot be pre-assigned in advance as any hidden variable theory would demand.
聽
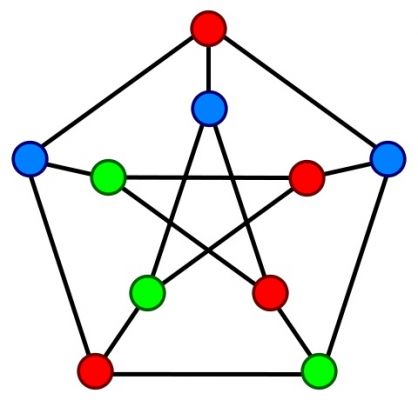
Fine, but what this has to do with graph theory? Represent any experiment you can do on a quantum system by a point in a two dimensional plane. If any two experiments are incompatible, draw a line between them. This forms a graph. If the result of an experiment is true, color its dot green. Color all the other statements linked by it red. Can you color the entire graph consistently? If yes, you have a classical graph. If no, you have a quantum graph.
聽
The simplest quantum graph is a pentagon (it takes too long to explain why a triangle is not the simplest case.). To color it consistently each green has to be sandwiched by reds, and each red has to be sandwiched by greens (a line switches the state between nodes). Try to do this for all 5 points. One dot will have to be both red and green.
聽
So what is the big deal? This is kindergarten stuff. Well, it turns out that there is an entire community of mathematicians who are experts in graph theory. And they can define and compute three numbers for any graph: "the independence number", "Lovasz theta number", and the "fractional packing numbers". And they have computer programs able to compute those numbers for any arbitrary graph.
聽
And now hold on for the punch line: the three numbers correspond to the Bell limit, the Tsirelson bound, and the Popescu Rohrlich bound in quantum mechanics. As a caveat, in some cases there is an ambiguity and one of the numbers' computational algorithm has to be modified slightly.
聽
Now the two communities of physicists and mathematicians were completely unaware of each others domain, and after the shock wore off, a frantic experimental work began to double check all these new bounds in the lab. This was followed by a systematic analysis of all graphs, and the largest Bell-type inequality violation was found, as well as cases where the Tsirelson bound was the same as the PR bound.
聽
So the low hanging fruits were already taken. Now it begins the work of making sense of why those numbers have a quantum mechanics meaning. In other words, what is the Lovasz number and why is this relevant for nature? In the end maybe we would get a deepened understanding of quantum mechanics.