Watching the Watchmen: Demystifying the Frauchiger-Renner Experiment — musings from Lidia del Rio and more at the 6th FQXi Meeting

Even by their usual excitable standards, the physicists and philosophers who study the foundations of quantum mechanics have been abuzz about a thought experiment first proposed in 2016 by Daniela Frauchiger and Renato Renner at ETH Zurich, and later published in Nature Communications (Frauchiger, D., Renner, R. Quantum theory cannot consistently describe the use of itself.聽Nat Commun聽₉,聽3711 (2018)). A blog post about it by Scott Aaronson of the University of Texas drew nearly 300 comments, and sparks flew at the two most recent FQXi meetings. So it was high time for me to buckle down and make sense of the experiment.

You can listen to a detailed rundown of the thought experiment for beginners, in which Renner talks through each step, on the podcast. He also describes the controversy his paper caused, and how fans of various interpretations of quantum mechanics--including Many World's, QBism, Bohmian mechanics and Collapse models--argue that the paradox actually supports their preferred model, while ruling out its rivals. But Renner, as you'll hear, disagrees, explaining that in his opinion, no current interpretation can provide a satisfactory way out of the paradox.

I've come up with my own way of describing it--vetted by Renner--and put it into the form of a quantum circuit that I've run on IBM's cloud quantum computer. Renner says it is the first experimental implementation of his experiment. (A closely related experiment proposed by 膶aslav Brukner of Institute for Quantum Optics and Quantum Information in Vienna has already been performed (Science Advances聽 20 Sep 2019: Vol. 5, no. 9, eaaw9832).) The interpretive dispute will no doubt rumble on. But what makes quantum physics fun is the journey, not the destination.

The experiment engineers a contradiction between third- and first-person views: the objective perspective that physics traditionally provides and the experience of an embedded observer. "In physics we try to build a theory of the world as seen from the outside, as God would see it," Renner's colleague L铆dia del Rio said at this year's FQXi meeting in Tuscany. "But of course, to do this, we have only, as a basis, our own observations. We are always talking about the point of view of some observers, and the best we can do is talk to each other, compare observations, and try to build a consistent picture." In the Frauchiger-Renner experiment, observers find themselves weirdly unable to do this. "The agents will make some inferences about each other's results, which in the end will be contradictory," del Rio said.

[youtube:Ls3RZpFgm3U, 560, 315]

These days, especially, it seems na茂ve to expect that we could reach consensus through dialogue. But et tu, physics?

_{Becoming One With Nature}

As usually presented, the experiment involves a convoluted series of measurements and logical deductions. But stripped to its essence, all you are doing is measuring a pair of entangled particles in two different ways. Normally, the first measurement of a particle would disturb it, spoiling the second. But Frauchiger and Renner propose a trick to measure and remeasure the particle in its pristine state: combine a direct and an indirect measurement. One observer measures the particle, and another measures the first observer. The first measurement transfers the state of the particle to the combined system of particle and observer, making it available for a second look. Frauchiger and Renner argue that, in specific cases, the indirect measurement is just as good as a direct one.

So, this experiment has the feature that observers are themselves observed. In most presentations of the experiment, the observers are human beings, but they could be just particles. All they have to do is make a prediction on the basis of quantum theory, and, for Frauchiger and Renner's scenario, that is a simple logical operation. Swapping particles for people makes the whole business of observing-the-observer seem less mysterious and implausible. That said, it also lessens the philosophical puzzle, because only if the observers are people can they be said to have a first-person viewpoint.

This procedure requires four observers in all, two for each of the entangled particles. Let's call those making the direct measurement the "friends" and those making the indirect measurement the "Wigners," in homage to the physicist Eugene Wigner, who was one of the first to note that observing the observer is a useful test case for interpretations of quantum theory. If the particles are photons, the observers measure their polarization using a special light filter. The friends orient their filters horizontally, and the particle either passes through (0) or reflects off (1). The Wigners orient theirs diagonally, and again the particle either passes through (+) or reflects off (-). So, that's four results to compare:

1. What a friend saw for the first particle vs. what a friend saw for the second

2. What a Wigner saw for the first particle vs. what a friend saw for the second

3. What a friend saw for the first particle vs. what a Wigner saw for the second

4. What a Wigner saw for the first particle vs. what a Wigner saw for the second

The team creates and measures multiple pairs of particles to see the statistical trends. The particles are entangled in a way devised by Lucien Hardy of the Perimeter Institute in 1993. This state can be written in four equivalent ways corresponding to the above cross-comparisons:

1. |00> + |01> + |10>

2. |+0> + |+1> + |-1>

3. |0+> + |1+> + |1->

4. |++> + |+-> + |-+> - |- ->

To write these is just an exercise in geometry, using the fact that diagonal is part horizontal and part vertical. I am neglecting the exact probabilities for these sundry outcomes; Hardy considered a range of values. What's important is that, in the first three formulas, only three of the four possible outcomes arise, whereas in the fourth all can occur. Hardy showed that such a pattern is hard to explain and seems to require some spooky coordination among the particles.

Frauchiger and Renner have a different aim. They don't seek to explain how the particles could exhibit this pattern, only what happens if they do. Because the first three formulas contain a restricted set of outcomes, a friend can sometimes be certain what a Wigner will see, and vice versa. Based on that, we can draw some conclusions for what they will see and surmise.

When the first friend measures 0, she can conclude the second Wigner will measure + (per #3).

When the second friend measures 1, she knows the first friend must have measured 0 (per #1) and concluded that the second Wigner will measure +. The second friend adopts this prediction as her own, on the assumption that if you know that someone knows something, you know that thing, too--a principle that philosophers call "closure."

When the first Wigner measures -, he knows the second friend must have measured 1 (per #2). He now adopts the friend's prediction.

But sometimes when the first Wigner measures -, the second Wigner will measure -, too (per #4). That violates the prediction. Paradox!

_{Winding Back the Clock}

When critics such as Aaronson say Frauchiger and Renner got it wrong, they are not disputing that the experiment gives the results it does. It's the interpretation that riles them.

Many have latched onto the strange feature that the observers are themselves observed. Observation is not a passive operation, but a thoroughgoing alteration. In the course of doing their indirect measurement, the Wigners undo the friends' direct measurement and wipe their memory. The friends see something, then un-see it. To them, it is as though nothing has happened; when the experiment wraps up and everyone else goes out for after-work drinks, the friends are still sitting there asking, "When will the experiment start?" In some descriptions of the experiment, it's even worse: they enter a Schr枚dinger-cat-like state of complete ambiguity. This makes The Matrix or brain-in-vat scenarios look tame by comparison. It's one thing to imagine that our world is a virtual projection, another that someone could reach directly into our brains and decide what we think.

At the meeting in Tuscany, Aaronson and Raphael Bousso at U.C. Berkeley argued that if you can't trust in your own integrity as a reasoning agent, you shouldn't be surprised to encounter contradictions such as the one in Frauchiger-Renner. By screwing with the friends' temporal continuity, the experiment smashes the chain of logical statements. If someone has made an observation and then un-made it, you can't base any conclusions on that observation.

Renner and del Rio reply that the experiment is staged to avoid this problem. The friends do get wiped, but by that point, they have no further role to play in the experiment. Whatever they saw and concluded has already been incorporated into the analysis, and nobody refers to it again. Now, you might wonder, if their memory is wiped, then how can any record of their observation endure? This is the most critical part of the experiment. Most of the time, it is true that no record endures. But when the conditions I laid out above are satisfied--namely, when observers are able to make definitive predictions for one another--information lives on. That happens for one in six trials (given the specific Hardy state used by Frauchiger and Renner), and a contradiction arises in half those cases. Thus the experiment walks a line: in undoing an observation, it sometimes preserves a trace of it.

_{Making the Circuit}

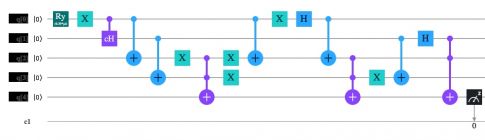
This can be illustrated by a quantum circuit--that is, an algorithm that can be implemented on a quantum computer. If you're new to quantum circuits, this section will probably make zero sense. The main takeaway is that the circuit shows how the observers don't need to be humans. Also, the circuit lays bare the sequence of events and the conditions under which information can endure, allaying some of the skeptics' misgivings.

I've implemented the circuit using Quirk, an online quantum simulator created by Craig Gidney in Google's quantum-computing group. (Gidney has his own circuit version of the Frauchiger-Renner experiment.) You can run and modify the circuit for yourself.

I'm attaching a PDF version of this circuit to this post. If you scroll down to the bottom of the post, you can click "Quirk_circuit.pdf" to open a larger version, so you can more easily see the details.

Here, the observers are abbreviated F1 and F2 (the friends) and W1 and W2 (the Wigners). The first two wires (horizontal lines) are qubits representing the entangled particles. The next two are flags indicating whether a given observer is able to make a firm prediction. The following two are the actual predictions. Although we have four observers, we need only two sets of wires, since we track only two observers at a time. The bottom wire is a workspace where observers compare their results and confirm they are entitled to make the inferences they do--an aspect of the Frauchiger-Renner experiment that tends to get overlooked.

Quirk has a nice set of probes--colored green or cyan--that show the qubit values and their correlations at any stage nondestructively. The two boxes with four little yellow circles are custom operations to create or manipulate the Hardy state. The rest of the symbols are standard quantum circuit symbols.

The steps in the procedure are:

1. Hardy state preparation

2. F1 measures particle 1. If 0, F1 is able to make a firm prediction--namely, that W2 will measure + (0). Otherwise F1 assigns equal probabilities to + (0) and - (1).This gives formulation #3 of the Hardy state.

3. F2 measures particle 2. If 1, F2 is able to make a firm prediction--namely, that F1 measured 0. Otherwise F1 assigns equal probabilities to 0 and 1. This gives formulation #1 of the Hardy state.

4. If F2 does make a firm prediction for F1, she can further conclude that F1 has made a firm prediction for W2--namely, that W2 will measure + (0)--and hence can provisionally adopt that prediction as her own. Because of the sign conventions adopted in this circuit, F2's prediction for F1 (in the 0/1 basis) is automatically a prediction for W2 (in the +/- basis).

5. F1 and F2 confer and check for two errors. First, whether, when F2 is able to make a firm prediction for F1 and W2, F1 either (i) could not make a firm prediction for W2, or (ii) made a different prediction. This tests the assumption of transitivity of knowledge. Note that F2 can adopt a prediction only if it is firm; if she tried to adopt probabilistic predictions, the next step would fail. A firm prediction can be made without using two-qubit gates. This selective reasoning is the main asymmetry in the experiment.

6. F1's role is over, so her measurement can be undone, clearing the way for W1 to make his. F1's prediction qubits can be put to other uses.

7. W1 measures particle in the +/- basis. If - (1), W1 is able to make a firm prediction--namely, that F2 measured 1. Otherwise W1 assigns weighted probabilities to 0 and 1. This gives formulation #2 of the Hardy state.

8. If W1 does make a firm prediction for F2, she can further conclude that F2 has made a firm prediction for F1 and thus for W2 and hence can provisionally adopt that prediction as her own. Because of the sign conventions in this circuit, we have to invert W1's prediction for F2 in order to interpret it as a prediction for W2.

9. W1 and F2 confer and check whether, when W1 is able to make a firm prediction for F2 and W2, F2 either (i) F2 could not make a firm prediction for W2, or (ii) made a different prediction. As in step #5, W1 can adopt only a firm prediction or else the next step would fail.

10. F2's role is over, so her measurement can be undone, clearing the way for W2 to make his.

11. W2 measures particle 2 in the +/- basis and obtains statistics for formulation #4 of the Hardy state, including -- (11) one run in 12.

12. W1 and W2 confer and check whether W1 erred, i.e. whether he predicted + (0) with certainty yet W2 obtained 1 (-). And he did err for one run in 12, half his predictions.

Just for fun, and just because I could, I ran this circuit on the IBM Q Experience online quantum computer. IBM's interface is sleek and easy to use, but I had to strip down the circuit to accommodate the hardware's limitations, not all of which are documented. I'm grateful to Paul Nation at IBM's Quantum Computing group for his help. The output is now a single error bit signaling a paradox: the second Wigner didn't observe - (1) as the other observers had predicted.

First I ran the circuit on IBM's own simulator and got such an error in 86 of 1024 trials, closely matching the theoretical prediction of one in 12.聽Then I ran it on an actual quantum computer located in Ourense, Spain. It was just as easy as running the simulator and took less than a minute. I got 461 errors in 1024 trials. This higher value suggest that the device is rather noisy. The other processors that IBM makes available gave similar results. I also checked some of the intermediate values and, not surprisingly, the early steps roughly match theory, while later ones deviate significantly.

_{To Each His Own}

So, if the strange wiping of memory doesn't account for the paradox, what does? It comes down to the unpalatable choice between quantum physics and the objectivity of knowledge.

Quantum physics says the second friend does not--and could not--measure the second Wigner directly. If you can't measure something even in principle, most physicists would question whether that thing exists, in which case there isn't any such thing as a direct comparison of these two observers, and the observers commit a fallacy by pooling their knowledge to draw the comparison nonetheless. Yet pooling knowledge is what scientists do. They couldn't function otherwise.

If you accept quantum mechanics as hard fact, but then weaken the category of "hard fact," haven't you swallowed your own tail? Physicists created the theory and proved it experimentally by stringing together inferences. Every measurement they make is indirect--a long chain of "if this, then that" stretching from the state of a particle to a signal a human can perceive. Those who would give up objectivity to save quantum mechanics may lose both. (That said, maybe quantum mechanics has a theory of knowledge tucked inside it in the form of quantum Darwinism, see "The Evolution of Reality.")

Carlo Rovelli and others have argued for years that quantum mechanics is perspectival: there is no third-person view at all. They still accept some kind of postulate of consistency: observers' viewpoints may differ, but must mesh whenever they come into contact, so that no out-and-out contradiction arises. Yet they remove the most natural explanation for that consistency: a world independent of us. Frauchiger and Renner's experiment might nudge more people to adopt a perspectival view, but heightens the puzzle of how we ever come to any agreement.