
Max Tegmark
Imagine you could feed the data of the world into a computer and have it extract the laws of physics for you. At the recent Foundational Questions Institute meeting, in Tuscany, FQXi director Max Tegmark described two machine systems he and his grad students have built to do exactly that. One recovers algebraic formulas drawn from textbook physics problems; the other reconstructs the unknown forces buffeting particles. He plans to turn his systems loose on data that have eluded human understanding, trawling for new laws of nature like a drug company screening thousands of compounds for new drugs."It would be cool if we could one day discover unknown formulas," Tegmark told me in a coffee break.
"One day" may already be here. Three theorists recently used a neural network to discover a relation between topological properties of knots, with possible applications to quantum field theory and string theory (V. Jejjala, A. Kar & O. Parrikar arXiv:1902.05547 (2019)). Machine learning has analyzed particle collider data , quantum many-body wavefunctions, and much besides. At the FQXi meeting, Andrew Briggs, a quantum physicist at Oxford, presented an A.I. lab assistant that decides how best to measure quantum effects (D. T. Lennon et al, arXiv:1810.10042 (2018)).聽 The benefits are two-way: not only can A.I. crack physics problems, physics ideas are making neural networks more transparent in their workings.
Still, as impressive as these machines are, when you get into the details, you realize they aren't going to take over anytime soon. At the risk of stroking physicists' egos, physics is hard--fundamentally hard--and it flummoxes machines, too. Even something as simple as a pendulum or the moon's orbit is a lesson in humility. Physics takes a lot of lateral thinking, and that makes it creative, messy, and human. For now, of the jobs least likely to be automated, physics ranks up there with podiatry. (Check the numbers for yourself, at the Will Robots Take My Job? site.)
Survival of the Fittest
Fitting an algebraic formula to data is known as symbolic regression. It's like the better-known technique of linear regression, but instead of computing just the coefficients in a formula--the slope and intercept of a line--symbolic regression gives you the formula itself. The trouble is that there are infinitely many possible formulas, data are noisy, and any attempt to extract general rules from data faces the philosophical problem of induction: whatever formula you settle on may not hold more broadly.
Searching a big and amorphous space of possibilities is just what evolution does. Organisms can assume an infinity of possible forms, only some of which will thrive in an environment. Evolution finds them by letting a thousand flowers bloom and 999 of them wither. Inspired by nature, computer scientists developed the first automated symbolic regression systems in the 1980s. The computer treats algebraic expressions as if they were DNA. Seeded with a random population of expressions, none of which is especially good at reproducing the data, it merges, mutates, and culls them to refine its guesses.
As three pioneers of the field, John Koza, Martin Keane, and Matthew Streeter, wrote in Scientific American in 2003, evolutionary computation comes up with solutions as inventive as any human's, or more so. Genetic-based symbolic regression has fit formulas to data in fluid dynamics, structural engineering, and finance. A decade ago, Josh Bongard, Hod Lipson, and Michael Schmidt developed a widely used package, Eureqa. They used to make it available for free, but now charge for it--as well they might, considering how popular it is at oil companies and hedge funds. Fortunately, you can still do a 30-day trial. It's fun to watch algebraic expressions spawn and radiate in a mathematical Cambrian explosion.
But the algorithm still requires additional principles to narrow the search. You don't want it to come up with just any formula; you want a concise one. Physics, almost by definition, seeks simplicity within complexity; its goal is to say the most with the least. So the algorithm judges candidate formulas by both exactness and compactness. Eureqa occasionally replaces complicated algebraic terms with a constant value. It also looks for symmetries--whether adding or multiplying by a constant leaves the answer unchanged. That is trickier, because the symmetry transformation produces a value that might not be present in the data set. To make an educated guess at hypothetical values, the software fits a polynomial to the data, in effect performing a virtual experiment.
Feynman in a Box
Tegmark and his MIT graduate student Silviu-Marian Udrescu take a different approach they call "A.I. Feynman" (arXiv:1905.11481 (2019)). Instead of juggling multiple possibilities and gradually refining them, their system follows a step-by-step procedure toward a single solution. If the genetic algorithm is like a community of scientists, each putting forward a particular solution and battling it out in the marketplace of ideas, A.I. Feynman is like an individual human methodically cranking through the problem.
It works by gradually eliminating independent variables from the problem.聽 "It uses a series of physics ideas... to iteratively transform this hard problem into one or more simpler problems with fewer variables, until it can just crush the whole thing," Tegmark told the FQXi meeting. It starts by looking for dimensionless combinations of variables, a technique particularly beloved of fluid dynamicists. It tries obvious answers such as simple polynomials and trigonometric functions, so the algorithm has an element of trial and error, like a human. Then it looks for symmetries, using a mini neural network instead of a polynomial fit. Tegmark said: "We train a neural network first to be able to approximate pretty accurately the function.... That gives you the great advantage that now you can generate more data than you were given. You can actually start making little experiments." The system tries holding one variable constant, then another, to see whether they can be separated.
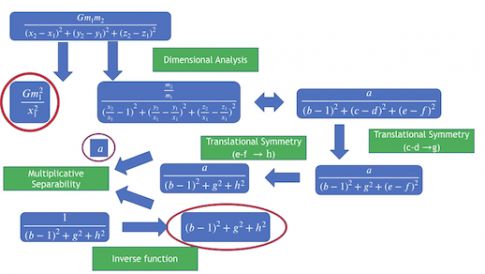
Credit: Max Tegmark
Udrescu and Tegmark tested their system on 100 formulas from the Feynman Lectures. For each, they generated 100,000 data points and specified the physical units of the variables. The system recovered all 100 formulas, whereas Eureqa got only 71. They also tried 20 bonus problems drawn from textbooks that strike fear into the hearts of physics students, such as Goldstein's on classical mechanics or Jackson's on electromagnetism. The system got 18; the competition, three.
To be fair, Eureqa is not the only genetic symbolic-regression system out there, and Udrescu and Tegmark did not evaluate them all. Comparing machine systems is notoriously fraught. All require a good deal of preparation and interpretation on your part. You have to specify the palette of functions that the system will mix and match--polynomials, sines, exponentials, and so on--as well as parameters governing the search strategy. When I gave Eureqa a parabola with a touch of noise, it offered x2 only as one entry in a list of possible answers, leaving the final choice to the user. (I wasn't able to test A.I. Feynman because Udrescu and Tegmark haven't released their code yet.) This human element needs to be considered when evaluating systems. A tool is only so good as its wielder.
Sorry to report, but symbolic regression is of no use to students doing homework. It does induction: start from data, and infer a formula. Physics problem sets are exercises in deduction: start from a general law of physics and derive a formula for some specified conditions. (Maybe more homework problems should be induction--that might be one use for the software.) As contrived as homework can be, it captures something of how physics typically works. Theorists come up with some physical picture, derive some equations, and see whether they fit the data. Even a wrong picture will do--indeed, one might argue that genuine novelty can arise only through an error. Kepler did not produce his namesake laws purely by crunching raw astronomical data; he relied on physical intuitions, such as occult ideas about magnetism. Once physicists have a law, they can fill in a new picture.
Or at least that is how physics has been done traditionally. Does it seems so human only because that is all it could be, when humans do it?
Making a Difference Equation
A formula describes data, but what if you want to explain data? If you give symbolic regression the position of a well-hit baseball at different moments in time, it will (if you get it to work) tell you the ball follows a parabola. To get at the underlying laws of motion and gravity takes more.
Since the '80s physicists and machine-learning researchers have developed numerous techniques to model motion, as long as it is basically Newtonian, depending only on the objects' positions and velocities and on the forces they exert on one another. If the objects are buffeted by random noise, the machine does its best to ignore that. Its output is typically a difference equation, which gives the position at one time given its position at earlier time intervals. This equation treats an object's path as a series of jumps, but you can infer the continuous trajectory that connects them, thereby translating the difference equation into a differential equation, as the laws of physics are commonly expressed.
Eureqa attacks the problem using genetic methods and can even tell an experimentalist what data would help it to decide among models. It seeds its search not with random guesses but with solutions to easier problems, so that it builds on previously acquired knowledge. That speeds up the search by a factor of five.
Other systems avail themselves of newer innovations in machine learning. Steven Brunton, Nathan Kutz, Joshua Proctor, and Samuel Rudy of the Univeristy of Washington rely on a principle of sparsity: that the resulting equations contain only a few of the many conceivable algebraic terms. That unlocks all sorts of powerful mathematical techniques, and the team has recovered equations not only of Newtonian mechanics but also of diffusion and fluid dynamics. FQXi'ers Lyd铆a del Rio and Renato Renner, along with Raban Iten, Tony Metger, and Henrik Wilming at ETH Zurich, feed their data into a neural network in which they have deliberately engineered a bottleneck, forcing it to create a parsimonious representation (arXiv:1807.10300 (2018)).
Pinball Wizard
Tegmark and his MIT grad student Tailin Wu hew closely to the methods of a paper-and-pencil theorist (Phys. Rev. E 100, 033311 (2019)). Like earlier researchers, they assume the equations should be simple, which, for them, means scrutinizing the numerical coefficients and exponents. If they can replace a real number by an integer or rational number without unduly degrading the model fit, they do. Tegmark told the FQXi meeting, "If you see that the network says, 'Oh, we should have 1.99999,' obviously it's trying to tell you that it's 2." In less-obvious situations, they choose whatever rational number minimizes the total number of bits needed to specify the numerator, the denominator, and the error that the substitution produces.
[youtube:9atnfAHBfSI, 560, 315]
Tegmark and Wu's main innovation is a strategy of divide-and-conquer. Physicists may dream of a theory of everything, but in practice they have a theory of this and a theory of that. They don't try to take in everything at once; they ignore friction or air resistance to determine the underlying law, then study those complications separately. "Instead of looking for a single neural network or theory that predicts everything, we ask, Can we come up with a lot of different theories that can specialize in different aspects of the world?" Tegmark said.

Credit Max Tegmark
Accordingly, their system consists of several neural networks, each covering some range of input variables. A master network decides which applies where. Tegmark and Wu train all these networks together. Each specialist network fits data in its own domain, and the master network shifts the domain boundaries to minimize the overall error. If the error remains stubbornly high, the system splits a domain in two. Further tweaking ensures the models dovetail at their boundaries. Tegmark and Wu do not entirely give up on a theory of everything. Their system compares the models it finds to see whether they are instances of the same model--for instance, a gravitational force law differing only in the strength of gravity.
Tegmark tested the system on what looked like a pinball ricocheting around an invisible pinball machine, bouncing off bumpers and deflecting around magnets. The machine had to guess the dynamics purely from the ball's path. You can see this demonstrated in Tegmarks' talk, about 4 mins into the YouTube video above. Tegmark and Wu tried out 40 of these mystery worlds and compared their system to a "baseline" neural network that tried to fit the whole venue with a single complicated model. For 36 worlds, the A.I. physicist did much better--its error was a billionth as large.
Think Different
All these algorithms are modeled on human techniques and suppositions, but is that what we really need? Some researchers have argued that the biggest problems in science, such as unification of physics and the nature of consciousness, thwart us because our style of reasoning is mismatched to them. For those problems, we want a machine whose style is orthogonal to ours.
A computer that works like us, only faster, will help at the margins, but seems unlikely to achieve any real breakthrough. For one thing, we may well have mined out the simple formulas by now. Undiscovered patterns in the world might not be encapsulated so neatly. For another, extracting equations from data is a hard problem. Indeed, it is NP-hard: the runtime scales up exponentially with problem size. (Headline: "It's official: Physics is hard.") A computer has to make simplifications and approximations no less than we do. If it inherits ours, it will get stuck just where we do.
But if it can make different simplifications and approximations, it can burrow into reaches of theory space that are closed off to us. Machine-learning researchers have achieved some of their greatest successes by minimizing prior assumptions--by letting the machine discover the structure of the world on its own. In so doing, it comes up with solutions that no human would, and that seem downright baffling. Conversely, it might stumble on problems we find easy. As Barbara Tversky's First Law of Cognition goes, there are no benefits without costs.
What goes on inside neural networks can seldom be written as a simple set of rules. Tegmark introduced his systems as an antidote to this inscrutability, but his methods presuppose that an elementary expression underlies the data, such as Newton's laws. That won't help you classify dog breeds or recognize faces, which defy simple description. On these tasks, the inscrutability of neural networks is a feature, not a bug. They are powerful precisely because they develop a distributed rather than a compact representation.聽And that is what we may need on some problems in science. Perhaps the machines will help the most when they are their most inscrutable.

Credit: Bart Selman
At the previous FQXi meeting in Banff, back in 2016, Bart Selman gave an example of how machines can grasp concepts we can't. He had worked on computer proofs of the Erd枚s discrepancy conjecture in mathematics. In 2014 a machine filled in an essential step with a proof of 10 billion steps. Its chain of logic was too long for any human to follow, and that's the point. The computer has its ways, and we have ours. To those who think the machine did not achieve any genuine understanding--that it was merely brute-forcing the problem--Selman pointed out that a brute-force search would have required 10349 steps. Although Terence Tao soon scored one for humanity with a pithier argument, he cited the computer proof as guidance. If this is any precedent, the hardest problems will take humans and machines side by side.