Quantum effects like entanglement or tunneling are increasingly believed to underlie biological processes. Yet quantum theory has explanatory depth beyond those phenomena: it provides novel conceptual means of attacking deep philosophical issues. Focusing on the role of quantum effects may obscure the potential for genuine philosophical innovation inherent in the quantum formalism. We identify four levels of quantum explanations: quantum effects, where a phenomenon is a direct result of quantum interactions; quantum consequences, where large-scale properties are reduced to quantum phenomena; quantum analogues, where essentially classical systems can profitably by modeled by a quantum description; and finally, quantum concepts, where quantum theory yields genuinely new explanatory approaches. Taking these into account throws new light on the role of quantum theory for life and mind.
Introduction
Quantum mechanics is widely—if somewhat misleadingly—believed to be a theory of the very small: atoms, perhaps molecules, in a pinch maybe the odd protein may fall under its ambit, but for anything larger, we typically expect a classical description to hold fast. Consequently, opposition to the idea that quantum effects are relevant for biological phenomena typically comes in the form of the 'large, warm and wet'-argument: for example, as Tegmark has estimated [1], coherence times in the environment of the brain are of the order of 10-20 to 10-13 seconds, roughly ten billion times faster than the millisecond timescale of relevant brain processes such as synaptic firing.
But true to Clarke's dictum that when the received view (abstracting away from his somewhat demeaning 'elderly scientist') declares something possible, it is almost certainly right, yet when it declares something impossible, it is very probably wrong, recent years have seen a considerable pushback on this idea. Biological phenomena such as avian magnetoreception [2], photosynthesis [3], and even cognition [4] (among others) have since emerged as plausible arenas for quantum effects to shape the development of life (and mind).
The explanatory heft of quantum theory in these phenomena is in providing what may be termed a 'generalized quantum advantage': in analogy to fields such as communication and computation, where the utilization of quantum resources confers quantitative gains, it is e.g. the efficiency of certain biological processes—such as that of electron transfer in photosynthesis—that finds its explanation in the quantum world. Like quantum computers, which outrank classical computers (for certain problems) in terms of speed, but are limited by the same boundaries of computability, quantum effects in biology are thus mainly appealed to as 'supercharging' certain processes. But it is not clear that this offers novel explanatory resources. In the somewhat polemic phrasing of Patricia Churchland, "pixie dust in the synapses is about as explanatorily powerful as quantum coherence in the microtubules" [5] (referring to the 'Orch-OR' proposal [6] for quantum cognition). Hence, does such quantitative quantum advantage exhaust the explanatory novelty of quantum mechanics as applied to life, or can we go beyond it to genuine qualitative novelty?
The purpose of this essay is to argue that the answer to this latter question may well be yes, and relatedly, that exclusive focus on quantitative quantum advantage may well obscure this transformative potential (without in any way intending to disparage the highly original and interesting research done in the field of quantum biology). My aim here is thus not to produce or defend a new explanation for any given (biological) phenomenon, but rather, to study the power of quantum theory as a novel explanatory framework. To this end, I will outline a taxonomy of potential explanatory uses of quantum theory, and evaluate their potential to shed light on difficult technical and conceptual problems at the intersection of science and philosophy. While they are not fully distinct, it is useful to think of four 'levels' of explanation:
-
The Schrödingerian level: phenomena that are a direct consequence of quantum effects. Most proposals in quantum biology so far fall unter this rubric.
-
The Feynmannian level: macroscopic phenomena that find their ultimate explanation only on the level of quantum mechanics, despite the absence of overt quantum effects.
-
The Bohrian level: applications of quantum-like formalisms/'quantum analogues' (such as generalized probabilistic theories) to classical systems.
-
The Paulian level: making use of the novel concepts intimated by the quantum formalism to clarify classically hard to explain phenomena, that is, understanding the quantum formalism as a genuinely transformative explanatory resource.
The main thrust of the argument outlined here is that, while the greatest potential for novel scientific findings arguably resides at the first level, it is the fourth that offers conceptual resources that shed new light on previously mysterious issues: quantum mechanics, beyond producing phenomena surprising to a classical world view, offers up new ways of thinking about the world that are scarcely imaginable without it. Hence, it provides a—still arguably largely untapped—resource of progress on questions that have engaged the best minds for centuries without any clear answers emerging.
Schrödinger: Quantum Life
One of the earliest notable forays into the relevance of quantum effects for biology came in Erwin Schrödinger's 1944 book What Is Life? The Physical Aspect of the Living Cell [7]. Schrödinger's aim was, in part, to elucidate the mechanisms for heredity and mutation. Looking at both of these phenomena, we encounter a seeming contradiction. Heredity requires that genetic material be extraordinarily stable, lasting through centuries of inheritance despite being subject to the destabilizing effects of Brownian bombardment from the thermal motion of particles in its environment. A classical physicist, Schrödinger argues, would be at a loss to explain this stability; but quantum physics, through the theory of the covalent bond, provides a ready explanation.
But this risks getting more than we bargained for: while genetic material needs to be stable enough to last through a great many rounds of cell division and transmission, it is also imperative that it must allow for a spontaneous variability, to enable mutation and thus, differential selection—evolution, in a word. Schrödinger points out that quantum systems typically have access to a discrete set of states, and that a molecule, settled into its lowest energy state, requires a certain minimum energy to be 'lifted' out of it—as opposed to a classical system, whose continuum of states can be transformed into one another by arbitrarily small perturbations. But in the quantum world, there is always a probability for a spontaneous, discontinuous 'quantum jump' between such different configurations.
Hence, Schrödinger found in quantum mechanics both an explanation for the stability of genetic information and the possibility of mutations. The form of this explanation provides the paradigm case of a quantitative quantum advantage: a molecule that would succumb to statistical fluctuations in the classical case has its stability enhanced by quantum effects. The same form of explanation is seen, e.g., in the quantum theory of photosynthesis: almost every photon incident on the light-harvesting complex of a chloroplast is transformed into chemically usable energy. For this to work, the energy must be transported across a series of neighboring light-receptive structures ('chromophores') to a reaction center. However, modeled as a classical stochastic process, randomly hopping between sites, this would be a very lossy transport route; but quantum coherence effects may provide the needed boost to explain the observed efficiency.
Most current applications of quantum mechanics to biology are of this form: classically inefficient or infeasible processes are enhanced by quantum mechanical effects, thus providing a boost to biological systems making use of them. But quantum theory's explanatory potential does not end here.
Feynman: Quantum Action
It is a bit of a puzzle why the 'large, warm and wet'-argument against the relevance of quantum mechanics to phenomena at the macroscopic level ever enjoyed much popularity. While an argument like Tegmark's might rule out the relevance of quantum effects for certain systems in a direct way, it is a fallacy to conclude, from there, that quantum mechanics has nothing to offer in terms of explanation. Indeed, counterexamples to this idea were known essentially from the beginning of quantum mechanics: the proposal of discrete, 'quantized' orbits of electrons around nuclei, due to Bohr, was to answer the puzzle that classically, an orbiting electron should continuously emit energy in the form of electromagnetic radiation and spiral into the nucleus. Thus, that matter is stable at all, and everything around you doesn't just spontaneously vanish in a burst of radiation, finds its explanation only at the quantum level.
But its stability is not the only property of matter that has a quantum explanation. In the metaphysics of Descartes, matter is res extensa—'extended stuff'. That is, its fundamental characteristic is that it takes up space, and that any given piece of matter can only be where other matter isn't. As argued by Dyson in the 1960s [8], this and the related fact that two chunks of matter don't pass through one another (and hence, your coffee mug rests safely on your desk) is ultimately due to the fact that certain kinds of quantum particles—fermions—can't ever precisely occupy the same quantum state: they obey what Pauli called the exclusion principle. As you try to bring them closer together, they will react with a certain pressure, resisting the attempt. On the other hand, bosons such as photons show no such penchant for keeping their distance: they will readily pool together, which is how you get lasers.
That matter is stable and extended—surely its most obvious and indeed defining characteristics—thus finds an explanation in quantum theory; however, this does not entail the presence of (coherent) quantum effects at macroscopic scales. Hence, quantum mechanics can be explanatorily relevant even in the absence of overt quantum phenomena. Moreover, these explanations are not of the 'quantum advantage'-kind: rather, they show how quantum mechanics makes possible what classical physics could at best take as a posit, since there, stable and extended matter is simply taken as given. Another example will show how quantum explanations can go beyond even that, elucidating what seems ineluctably mysterious in a classical setting.
A ray of light, traversing multiple media, will take the path that minimizes the traversal time (Fermat's principle). This opens up a puzzling question: how does the ray of light know which of the potential paths available to it is the one of smallest duration? More generally, physical systems behave such that their motion minimizes a quantity known as the action—which roughly tracks the balance between kinetic and potential energy along a trajectory. Again we are faced with a disturbing teleology: the path must be known before the first step is taken, so to speak. Here, it is Feynman who found the right (quantum) explanation [9]: relative differences in action lead to interference effects, such that where the action is small (and changes slowly), neighboring paths reinforce one another (in terms of their likelihood), while where the action is large, neighboring paths cancel each other out—i.e. the probability that a particle takes them becomes vanishingly small. At the macroscopic level, thus, with overwhelming likelihood, the path of least action is the one taken by the system.
This is a first example of a quantum explanation that does not offer merely a quantitative advantage: what seems classically unreasonable—that a particle might 'look ahead' and choose its best course—can be accounted for by appealing to quantum phenomena (albeit at the cost of making the principle a probabilistic rather than absolute one).
Bohr: Quantum Ubiquity
Quantum theory can be viewed as a particular generalization of probability theory to a noncommutative domain. But noncommutativity—that is, that the order of a sequence of operations matters for its result—does not only occur at the microphysical level. This opens up the possibility of using the quantum formalism to model phenomena within the regime of classical physics—where thus any noncommutativity is only effective, rather than mandated by the physics of the situation. Such situations, however, are rather ubiquitous: the result of putting on your underwear first, and then your pants, radically differs from the reversed procedure.

Figure 1 The Necker cube is an example of bistable perception, with either of the two sides lying in the image plane capable of being seen as 'front' and 'back'.
Of course, there is rather little use for a quantum description of dressing habits. But are there areas where such a description could offer a benefit? Indeed, there seem to be: consider the drawing in Fig. 1. The cube can be seen as having either of two orientations, labeled '0' and '1' in the image. Now consider the following experiment: a test person is asked, at two out of three points in time t1, t2, and t3—so at (t1, t2), (t2, t3) or (t1, t3)—to report whether they see orientation '0' or '1'. Call the results of these probes C1, C2, C3, each of which can take the value '0' or '1' to indicate the observed orientation.
We can then study the correlations of these observations: the quantity
⟨C1C2⟩=P(C1=C2)−P(C1=C2)
where P denotes probability, gives the degree to which both reports agree—e.g. a value of 1 signals perfect agreement, while -1 means both always take opposite values. We can then derive (see technical endnotes for details)
⟨C1C2⟩+⟨C2C3⟩+⟨C1C3⟩≥−1.
What is the meaning of this inequality? If the test person has, at every point in time, a definite perception of the cube as being either in orientation '0' or '1', then the above sum can never be smaller than -1. (It is immediately clear that e.g. the algebraic minimum, -3, cannot possibly be reached, because if C1 and C2 are perfectly anticorrelated, and C2 and C3 are, as well, then C1 and C3 must be perfectly correlated.)
What does noncommutativity have to do with definite values? Suppose we have two processes A and B (where each process might be 'measure quantity A/B'). Then we have
AB−BA=0.
That is (reading from right to left in the individual terms) carrying out process B before A yields a different result than carrying out process A before B. Suppose now that each of these processes merely yields a definite value a or b. Since this is just an ordinary number, we can exchange it with each process, yielding symbolically
AB−BA=AB−Ba=(A−a)B=(A−a)b=ab−ab=0,
in direct contradiction to our prior stipulation. This is the reason for the uncertainty principle in quantum mechanics: if two quantities (resp. their measurement processes) fail to commute, they cannot both simultaneously have definite values. Conversely, two quantities that have simultaneous values always commute.
Now, in psychological experiments, one indeed finds violations of inequalities closely related to the above [10], indicating the possibility that perceptual states do not always carry definite content. However, this should not be taken as evidence for genuinely quantum phenomena underlying human cognition: indeed, there is nothing greatly mysterious to noncommutativity at the cognitive level. In the phenomenon of priming, prior stimuli are well known to influence later behavior—just imagine being shown pictures of moldy fruit and then choosing your favorite food versus a reversed procedure: it is not hard to imagine differences in judgment (indeed, your appetite may have left you entirely in the first case).
Nevertheless, a recognition that the quantum formalism may offer an adequate description even in systems where noncommutativity is not guaranteed by the fundamental physics, but is instead an 'emergent' feature of a complex system, may offer important clues about the internal processes of that system—such as, against intuition, indicating that perceptual states may not always have definite content. An early proposal that can be read in this spirit is due to Niels Bohr.
Perhaps Bohr's chief philosophical innovation is the concept of complementarity. For our purposes, complementarity will simply mean that certain (sets of) quantities do not have simultaneously definite values, and hence, different descriptions are applicable to different contexts. The canonical example here is the wave- versus particle-picture: depending on the experimental setting, either of these, but not both together, may yield an appropriate description. From the above discussion, a connection to the noncommutativity of certain processes is clear.
Bohr applied his principle of complementarity beyond physics early on. In a lecture entitled Light and Life, delivered to the Second International Congress on Light Therapy in August 1932, he proposed that "the efforts of physicists to master [the quantum description of light] resemble in some way the attitude towards the aspects of life always taken more or less intuitively by biologists" [11]. Bohr's aim was thus markedly different from Schrödinger's: rather than grounding the phenomena of life in quantum mechanics, he sought an analogy between the biological and physical sciences, in order to use concepts developed within the latter to illuminate quandaries of the former.
Concretely, Bohr's subject was the—in those days still somewhat ongoing—debate between mechanism and vitalism as relates to the study of life. Mechanism holds that living organisms are nothing but complex machines; vitalism, on the other hand, posits that such an explanation fails to capture the full extent of vital phenomena. (It may be relevant here that Bohr's father, Christian Bohr, had himself been a prominent figure on the vitalist side.) Bohr's position, while clear in its rejection of both the vitalist and reductive mechanist picture, is difficult to disambiguate, but centered around an analogy to (physical) complementarity. (To give a crude approximation, the mechanistic mode of description is typically not available concurrently with the vitalistic one, since disarticulating a living organism into its mechanical parts is generally not conducive to its continued well-being.) We will not propose here to enter further into Bohr exegesis, and instead merely note that this analogical character of explanation constitutes an explanatory appeal to the quantum formalism distinct from the previous two.
Pauli: Quantum Qualia
Bohr's proposal is essentially epistemological in nature. But arguably, the lessons of quantum theory run deeper still, transforming our ontological concepts. Suppose that you have two at least on first blush separate sets of phenomena—waves and particles, life and non-life, mind and matter. It appears a simple exercise in logic to figure out the ways these could be related. Using mind and matter as an example, these are shown in Fig. 2. In turn, they are: a) Leibnizian dualism, where both phenomena are essentially distinct and only a 'prestabilized harmony' accounts for their apparent connection; b) Cartesian interactionist dualism, where both domains mesh within a special nexus (the pineal gland according to Descartes); c) coincidence, where either every phenomenon has both mental and physical character (dual-aspect monism or panpsychism) or both are aspects of a third domain (neutral monism); d) reductionism, where either all mental phenomena are ultimately physical (materialism) or the other way around (idealism); e) eliminativism/illusionism, where one set of phenomena is merely apparent.
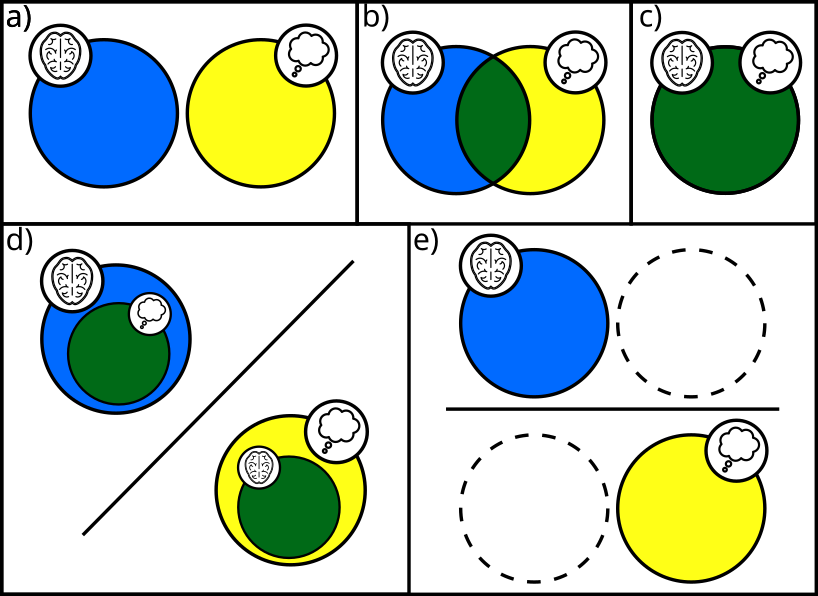
Figure 2. Possible relations between two sets of phenomena, using the example of mind and matter.
One might propose this taxonomy to be a priori, deducible from pure reason alone. Whatever phenomena one encounters must relate to one another in one of the above ways. Indeed, exactly this has been the historical argumentation: when George Boole laid out the ground rules of modern logic in the mid 19th century, he derived what he termed 'conditions of possible experience', noting that "[w]hen satisfied, they indicate that the data may have, when not satisfied they indicate that the data cannot have resulted from an actual observation." [12] These conditions take the form of inequalities—and indeed, the inequality presented above is just of this kind. More generally, Boole's conditions were rediscovered in the context of quantum mechanics by the Irish physicist John Stewart Bell (hence 'Bell inequalities') [13], and their experimental violation won the 2022 physics Nobel. Thus, contrary to Boole's declaration, we find that actual observation indeed fails to satisfy his conditions.
Boole's logic is the algebra of sets and subsets, with logical connectives such as 'AND' and 'OR' corresponding to set intersection and union, respectively. (For an illustration of the connection between Bell inequalities and the logic of sets, see [14].) What the failure of his conditions to be satisfied in the real world then indicates is that this logic cannot straightforwardly be extended across all domains—there are relations between phenomena that do not fit this characterization. It bears repeating: we have here an example of something that, before the development of quantum theory, would have been unquestionably accepted by most thinkers as a simple consequence of logic failing to apply to the real world. The relation of complementarity, which underlies each such violation, is something entirely new and previously unimagined. (This does not entail that one should replace classical logic with a 'quantum logic', as proposed by Putnam, alleging its 'empirical' character [15]. Rather, it should be understood as a caution on the applicability of supposedly 'a priori' deductions to physical reality.)
The question now is whether this discovery has consequences for everyday experience, or if it remains confined to a curiosity of the microworld. That the former is indeed the case was first proposed by Wolfgang Pauli, who in a 1952 letter to Rosenfeld wrote that "it would be most satisfactory if physis and psyche could be conceived as complementary aspects of the same reality." [16]
The problem of the relation between mind and body, between conscious experience and physical reality has vexed philosophers and scientists for centuries, infamously being dubbed simply 'the Hard Problem' by David Chalmers [17]. What Pauli's proposal intimates is that the hardness of this problem may be due to the fact that we have so far sampled possible explanatory models from the range of offerings as outlined in Fig. 2; however, quantum theory shows us that there are options realized in nature that go beyond these. Does this extend to the 'psychophysical relation'? As of yet, this question remains wide open. However, the mere fact that centuries of stalemate might be overcome by the presence of a genuinely new option on the table should be more than enough to warrant serious investigation.
How Quantum is Life?
Regarding the importance of quantum theory for life, this essay has been a plea to take into account its full explanatory potential. Life and mind as phenomena, and their relation to quantum theory, can be analyzed on multiple levels, and we stand only to gain by approaching them accordingly. As we have seen through both historical and contemporary examples, quantum theory offers explanatory power beyond quantitative advantages. Life might flow from, or make use of, quantum effects, but beyond that, novel concepts and possibilities intimated by quantum theory might shed new light on old questions. Perhaps most intriguingly, what was considered logically stringent before the quantum revolution forfeits its compelling character in the face of genuine qualitative novelty—options that have not been intuited before, and perhaps, could not have been.
In particular the still puzzling relation between mind and matter emerges as a potential candidate for quantum explanation beyond a generalized quantum advantage. Where classical models have stood in deadlock, circling through the selfsame set of options again and again, quantum theory puts a novel possibility onto the table: the relation of complementarity, that cannot easily be brought under the familiar gamut of classical possibilities governed by the logic of sets. If this relation obtains between mental and mechanical phenomena, the failure to satisfactorily elucidate their connection—the Hard Problem's hardness—becomes less puzzling: like waves and particles, each fails to be explicable in terms of the other, yet both are necessary for a complete picture.
At present, of course, these are highly speculative remarks. But wouldn't it be fantastic if the quantum could do for Cartesian res cogitans what it already has done for his res extensa?
[1] Tegmark, Max. "Importance of quantum decoherence in brain processes." Physical review E 61.4 (2000): 4194.
[2] Kominis, Iannis K. "The radical-pair mechanism as a paradigm for the emerging science of quantum biology." Modern Physics Letters B 29.Supplement 1 (2015): 1530013.
[3] Kassal, Ivan, Joel Yuen-Zhou, and Saleh Rahimi-Keshari. "Does coherence enhance transport in photosynthesis?" The journal of physical chemistry letters 4.3 (2013): 362-367.
[4] Fisher, Matthew PA. "Quantum cognition: The possibility of processing with nuclear spins in the brain." Annals of Physics 362 (2015): 593-602.
[5] Churchland, Patricia S., Stuart Hameroff, Roger Penrose. "Does Consciousness Emerge from Quantum Processes?" The Times Higher. (April 5, 1996)
[6] Hameroff, Stuart, and Roger Penrose. "Consciousness in the universe: A review of the ‘Orch OR’theory." Physics of life reviews 11.1 (2014): 39-78.
[7] Schrödinger, Erwin. "What is life?: With mind and matter and autobiographical sketches." Cambridge university press, 1992.
[8] Dyson, Freeman J., and Andrew Lenard. "Stability of matter. I." Journal of Mathematical Physics 8.3 (1967): 423-434.
[9] Feynman, Richard Phillips. "Space-time approach to non-relativistic quantum mechanics." Reviews of modern physics 20.2 (1948): 367.
[10] Atmanspacher, Harald, and Thomas Filk. "A proposed test of temporal nonlocality in bistable perception." Journal of Mathematical Psychology 54.3 (2010): 314-321.; Waddup, O.J., Yearsley, J.M., Blasiak, P. et al. "Temporal Bell inequalities in cognition." Psychon Bull Rev 30 (2023): 1946–1953.; Gronchi, Giorgio, and Elia Strambini. "Quantum cognition and Bell’s inequality: A model for probabilistic judgment bias." Journal of Mathematical Psychology 78 (2017): 65-75.
[11] Niels Bohr, "Light and Life." Nature 133 (1933): 457–459.
[12] Boole, George. "XII. On the theory of probabilities." Philosophical Transactions of the Royal Society of London 152 (1862): 225-252.
[13] Bell, John S. "On the Einstein Podolsky Rosen paradox." Physics Physique Fizika 1.3 (1964): 195.
[14] "The Meaning of Bell's Inequality", web resource, https://xseek-qm.net/Bells_inequality_e.html. Accessed 10.10.2025.
[15] Putnam, Hilary. "Is logic empirical?" Boston Studies in the Philosophy of Science: Proceedings of the Boston Colloquium for the Philosophy of Science 1966/1968. Dordrecht: Springer Netherlands, 1969.
[16] Atmanspacher, Harald. "Dual-aspect monism à la Pauli and Jung perforates the completeness of physics." AIP Conference Proceedings. Vol. 1508. No. 1. American Institute of Physics, 2012.
[17] Chalmers, David J. "Facing up to the problem of consciousness." Journal of consciousness studies 2.3 (1995): 200-219.
[18] Popescu, Sandu, and Daniel Rohrlich. "Quantum nonlocality as an axiom." Foundations of Physics 24.3 (1994): 379-385.
[19] Janas, Michael, Michael E. Cuffaro, and Michel Janssen. "Understanding quantum raffles." Springer International Publishing, 2022.