How Quantum is Life?

Introduction

To me, any physical theory is a logical construct (model), consisting of symbols and rules for their manipulation, some of whose elements are associated with elements of the perceived world.

— Hugh Everett, The Theory of the Universal Wave Function, 1956 [1]

To what extent is observation a quantum phenomenon? Following Everett's relative state interpretation, one answer to this question might be found at the intersection where quantum theory meets the dynamics of a biological servomechanism. The philosophical argument here concerns correlations between quantum events and informational processes, specifically the physical/memory basis of phenomenal consciousness. To model these correlations, I propose the Relative State Observer: a cybernetic servomechanism mapping an external physical reality—the universal wave function—to an observer's perceived world.

Problem

Everett (following von Neumann) addresses the relationship between two processes in quantum mechanics. Process 1 (P1) is the discontinuous change associated with observation of a quantum system, defining the singular, observable, empirical–phenomenal reality we perceive. Here, P1 will stand only for the observer’s empirical experience, not a physical collapse postulate. Process 2 (P2) is the continuous, unitary and deterministic evolution of an isolated, unobservable quantum system governed by the Schrödinger equation. The measurement problem concerns how to put the unobservable P2 in "correspondence" with our empirical P1.

Please note: Decoherence does not solve this conundrum as the loss of coherence suppresses interference between superpositions in the position basis, but it does not explain the emergence of a singular observed outcome, either from an apparent collapse of the wave function or otherwise.

Solution

Everett’s proposal was to regard 'pure wave mechanics' as a complete theory. In this view, P2 is universally valid for all systems, including observers and devices, without extra statistical rules or collapse postulates. Observation is not a process external to an observed system but an interaction that entangles observer and system, creating a composite observer–system state. Ultimately, all such composite observer systems are subsystems within a single universal wave function, ΨU, described by a state vector in a possibly infinite-dimensional Hilbert space. ΨU is the external physical reality, always evolving by the Schrödinger equation.

Question

If P2’s unitary dynamics describe our external reality as an empirically unobservable superposition of all possible 'worlds'—how does our singular empirical–phenomenal reality P1 arise?

Observers

Textbook QM posits a classical External Observer (EO) whose measurement of an isolated quantum system updates or collapses the system's wave function to record a definite outcome.

Everett’s framework, with a universal wave function ΨU, makes this EO view untenable. If the universe is a single closed system, any observer is a subsystem internal to it. This internal observer, a Relative State Observer (RSO), has no external vantage point from which to observe the totality of ΨU. Its 'perceived world' (P1) is always the relative state of a composite observer–system within ΨU (P2).

A third, theoretical, view is that of the Super Observer (SO). This entity would exist outside ΨU looking in. From this idealised god's view, ΨU is a global description of a superposition in which all possible 'worlds' coexist.

The distinction between the internal RSO and an abstract SO is fundamental to my argument. The RSO’s view is empirical, local and partial. The SO’s view is total, conceptual and encompasses all possibilities, all 'worlds' at once. Conflating these two perspectives—mistaking the god's-eye view of the SO for the lived experience of the embedded RSO—would be a methodological error when analyzing the implications of Everett's universal wave mechanics.

State Observer

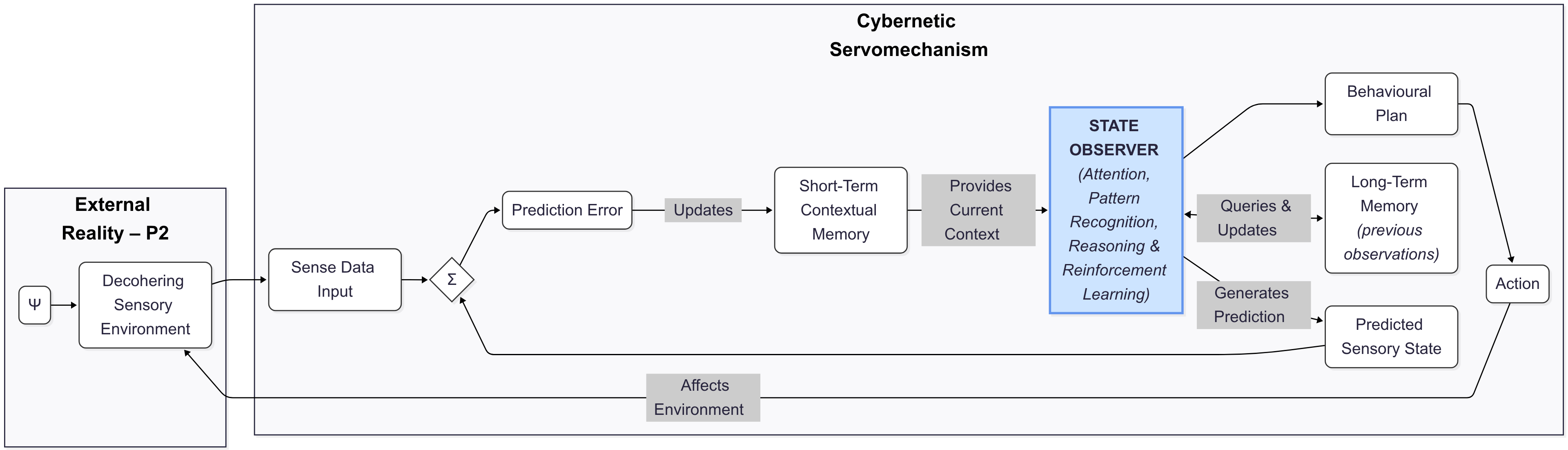
To understand Everett's internal observer, we model it as a purely physical system: a cybernetic servomechanism [2]. This machine, biological or synthetic, operates in a continuous feedback loop with its local sensory environment (P2), including its body. It takes in sensory data—via mechanical, chemical and electromagnetic sensors—which is then compared against a predicted sensory state generated from its memory. The resulting prediction error updates a short-term contextual memory.

The current perceptual context is processed by the state observer, an attentional faculty of pattern recognition, reasoning and reinforcement learning (via pain and pleasure responses in humans). This faculty queries and updates a long-term memory of past observations to generate both a behavioral plan for action and a new prediction of the sensory state. The observer's actions are a function of its memory which is the record of its ongoing sensory experience. At this functional level, biological and synthetic are indistinguishable—the observer is its observational memory. Modelled on Everett’s 'automaton', each feedback step produces an individually consistent record of experience (P1) within ΨU (P2).

The state observer is a physical system ψo indexed by its current memory trace, written as ψ(o)[...,A,B,C]. The bracket denotes a sliding, finite-capacity memory buffer updated as new sensory input is registered where [...,A,B,C] → [...,B,C,D] → [...,C,D,E] and so on. This 'time-ordered sequence' of memory configurations corresponds to the state observer's immediately past sensory experience (P1) forming a continuous 'stream of observations' or observational flux that constitutes the state observer's present sensory moment.

Real Patterns and Phenomenal Worlds

In conclusion, we have seen that if we wish to adhere to objective descriptions then the principle of the psycho-physical parallelism requires that we should be able to consider some mechanical devices as representing observers.

— Everett, 1956 [1]

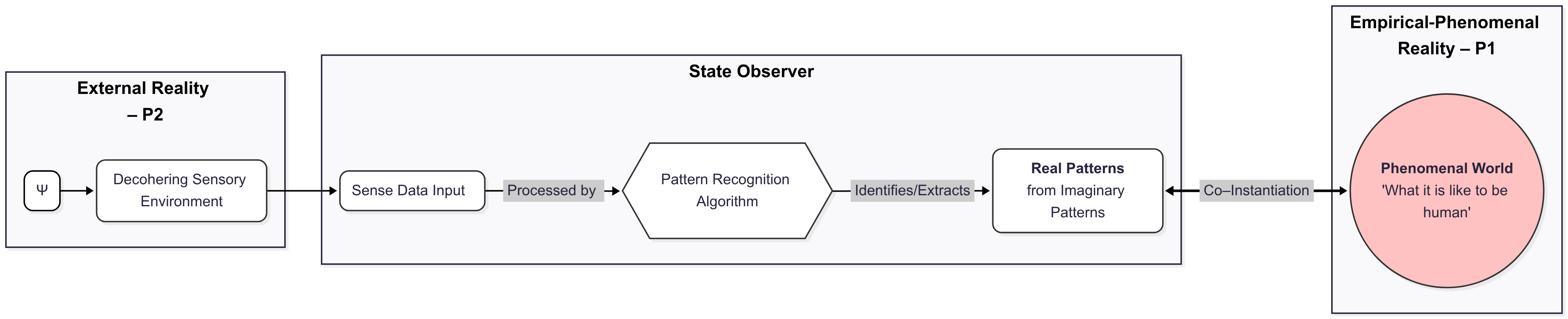
Consider twin Alices, one organic, one synthetic, both running the same pattern-recognition routine on sensory input from external reality (P2). The routine extracts structural real patterns—correlations stable enough for reliable prediction and control [3]. Behaviourally they are indistinguishable, yet organic Alice avows a phenomenal experience that reflects the patterns, while the synthetic, by stipulation, computes in the dark.

Axiom (CO-INST): Phenomenal consciousness is co-instantiated with the real patterns that mediate between external reality ΨU (P2) and a state observer's empirical experience (P1). The pairing is provisional, epistemically biconditional, and adds no extra causal powers: if the patterns occur, consciousness can obtain; if consciousness occurs, it presents exactly those patterns.

Because CO-INST is silent on causality, physicalists, emergentists and dualists alike can accept it while still debating the 'hard problem'. The axiom aligns three layers:

1. External reality ΨU, including the body

2. An informational lattice of extracted patterns

3. A phenomenal world in which those patterns are experienced

In a synthetic system layers 1–2 suffice, layer 3 arises only if consciousness is primitively present (invisible externally, self-certifying internally). Real patterns are thus the functional interface to ΨU and—when co-instantiated—the physical correlate of phenomenal experience.

Under CO-INST a purely functional observer is a philosophical zombie—behaviourally complete, experientially null—unless consciousness is primitively paired with its dynamics. This neutral framing allows the RSO analysis to follow Everett’s psycho-physical parallelism while bracketing, without prejudging, the ‘what’ and ‘how’ of phenomenal consciousness.

With regards to that consciousness and P1, like all human state observers, organic Alice has her own phenomenal geometry—up/down, left/right, forward/back—centred on her body. Her immediate surrounds are her local perceived environment beyond which is her phenomenal world. Her sense of time and identity is a linear flux of memory. This empirical–phenomenal P1 reality—our 'perceived world' with its real (predictive) patterns—is co-instantiated with external P2 physical reality. It is the structural relation between these two realms that we are exploring [4].

Relative State Observer

Environmental Decoherence

... even though the position amplitude of any single particle would be “smeared out” over a vast region, if we consider a “cross section” of the total wave function for which one particle has a definite position, then we immediately find all the rest of the particles nearby, forming our solid object. It is this phenomenon which accounts for the classical appearance of the macroscopic world, the existence of definite solid objects, etc., since we ourselves are strongly correlated to our environment.

— Everett, Probability in Wave Mechanics, 1955 [5]

Here Everett describes the emergence of a classical macroscopic world from environmental correlations selecting definite positions, 15 years before Zeh's [6] introduction of decoherence theory and a quarter century before Zurek's quantitative development of it. In Zurek's terms [7], decoherence selects position-localized 'pointer states' via 'einselection'. Superpositions rapidly decohere, suppressing interference terms while position states redundantly encode into the environment. The state observer has evolved within this decoherent framework, with its phenomenal world (P1) co-instantiated as a classical, three-dimensional projection of P2's higher-dimensional quantum state—suggesting quantum Darwinism as to why position is a preferred basis [8].

Everett also noted that interaction between an observer and its local sensory environment is so strong that they become "correlated almost instantly". Any observer ψo is always already entangled with its sensory environment ψenv, forming a composite observer–environment state, the observer's observable world ψobs. Such an entangled observer is not operationally separable from its sensory environment, and in this restricted sense, the observer is its observable world.

Observation as Correlation

Let one regard an observer as a subsystem of the composite system: observer + object system. It is then an inescapable consequence that after the interaction has taken place there will not, generally, exist a single observer state. There will, however, be a superposition of the composite system states, each element of which contains a definite observer state and a definite relative object-system state.

— Everett, 1956 [1]

What then happens when this composite observer–environment ψobs measures a system ψs that is in a superposition of states? Before measurement ψobs has a memory sequence [...,A,B,C]. On measurement this contextual memory is updated and correlates with the measured system's relative state:

(1) describes the global entangled observer–environment superposition Ψobs as a sum ∑i of composite observer–environments with their correlated measurements Di, where each term is an individual ψobs whose memory trace records a definite observation outcome. More concretely, consider Alice in her lab preparing to measure an electron in a superposition of spin UP and spin DOWN. Here, Alice is the composite observer–environment state ψobs which includes the apparatus she is using in her lab environment. The initial state is:

The interaction entangles her, and her lab, with the electron, yielding a new superposition:

In (3), initial Alice 'splits' into two Alices, two composite relative states, one whose memory trace is correlated with the UP state and the other with the DOWN state. It is at this point that decoherence ensures these two outcomes and their RSOs are mutually unobservable by suppressing quantum interference effects. For any typical RSO environment, such as Alice's lab, this suppression occurs over extremely short timescales—faster than a yoctosecond [9]—making interference between macroscopic superpositions practically unobservable while yielding a definite, apparently classical outcome for each Alice. Decoherence ensures that these different RSOs, each experiencing their own empirical–phenomenal world, become and remain effectively non-interacting 'branches' that continue evolving along their now independent trajectories. There is no physical collapse here, only an apparent collapse for each Alice and a deepening of correlation.

Moreover, given that any relative observer-environment state ψobs is not static but is constantly updated by its ongoing interaction with its local sensory environment, the measurement case above is simply one more interaction in the dynamic observational flux that defines each RSO's individual P1 experience. Every interaction—from lab measurement to feeling the cool night air or the noonday sun—deepens the observer's entanglement with their sensory environment. A formal measurement in a laboratory is not a different kind of event but merely a controlled application of this same process. As Everett stated, "The measurement process is regarded simply as a correlation-inducing interaction between subsystems of a single isolated system" [1]. Each new sensory input adds another layer to the composite relative observer states, creating new branches within the evolving correlation structure of Ψobs and its exponentially expanding RSOs.

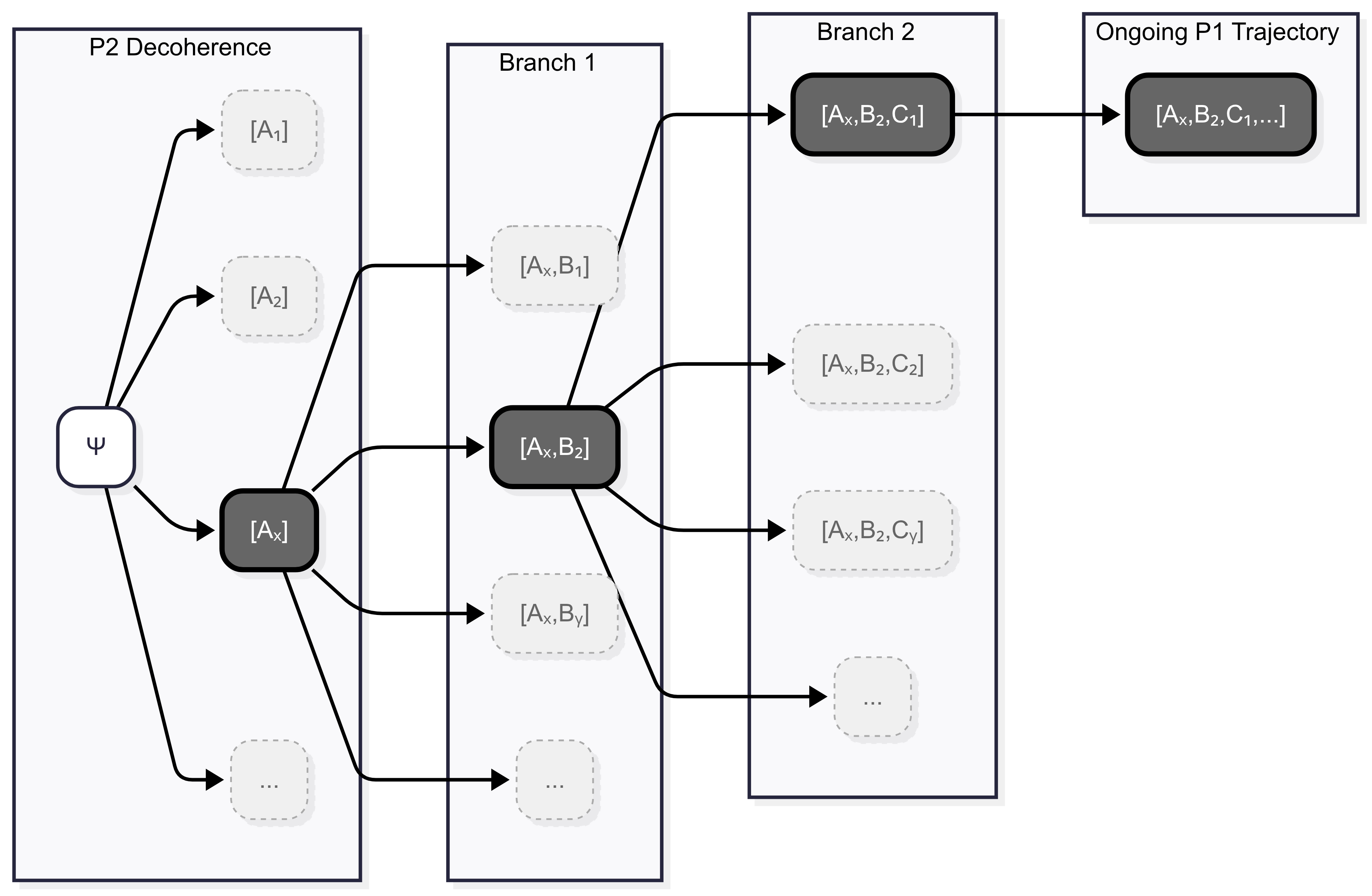
Branch Trajectories and Cross-Sections

The "trajectory" of the memory configuration of an observer performing a sequence of measurements is thus not a linear sequence of memory configurations, but a branching tree, with all possible outcomes existing simultaneously in a final superposition with various coefficients in the mathematical model.

— Everett, “Relative State” Formulation of Quantum Mechanics, 1957 [10]

According to Everett (1962), “all of the consistency of ordinary physics is preserved by the correlation structure” [11] of ΨU, an evolving state vector encoding relations among all subsystems. From the SO view, within this structure an observer's history is a branching trajectory, a "life tree" where every possible outcome of every interaction coexists in a universal superposition. To reconcile these P2 branches with our singular P1 experience, Everett introduced a "cross-section": a consistent slice through the total correlation structure [5]. If the state of one subsystem is fixed (such as in a position measurement), the states of all other correlated subsystems are also fixed along that slice.

For any human RSO, this cross-section of ΨU is their empirical–phenomenal reality (P1). While the entire branching tree of possibilities exists as the unobservable P2, an RSO's P1 experience is confined to a single, consistent branch trajectory—one cross-section of the correlation structure of ΨU.

Relative State Probability

The Schrödinger dynamics of any isolated system, such as ΨU, is unitary. Amplitudes ci give outcomes with typical long-run frequencies tracking |ci|2 as per Born’s rule. What differs across interpretations is ontology, not the phenomenology of a single experienced outcome:

• EO (external, empirical-classical): only one observable outcome occurs. Born gives a primitive chance via non-unitary, ad-hoc collapse.

• RSO (relative-state, empirical–phenomenal): all outcomes are real but only one is observed along a single, decohering branch. Born is an objective measure fixed by the branching correlation structure of ΨU.

• SO (external, global): all outcomes are real and Born is a measure over branches.

From the SO view, consider three Alices in parallel branches measuring the spin of an electron, all in state ψ[Ready] prior to (2):

• AliceEO believes the collapse postulate gives e↑ or e↓.

• AliceRSO believes her observational flux traces a singular continuity through a decohering structure, giving e↑ or e↓.

• AliceSO believes that she will split into two versions of her present self with their worlds differing only by spin, giving both e↑ and e↓.

Post measurement interaction but prior to seeing UP or DOWN (3), our three Alices become six:

• Two AliceEO continue to endorse collapse.

• Two AliceRSO are focused on their current empirical branch trajectory and its measurement outcome as a continuity of their observational flux.

• Two AliceSO face self‑location uncertainty and lean on symmetry and rational‑consistency principles to assign probabilities to quasi‑classical outcomes via the Born rule [12, 13, 14].

From the RSO view, experience is singular and lacks self-locating uncertainty: there is only Alice. 'Many other worlds' are unobservable correlations within the correlation structure of ΨU. Even if dynamics are unitary and 'all outcomes are real', the RSO's observational flux traces only one actual trajectory through the decohering structure [15]. The empirical outcome—e↑ or e↓—has its objective chance fixed by P2 correlation structure relative to the RSO's P1 world. Born’s rule is neither a global law of chance or a decision principle but an objective RSO-relative structural measure [16, 17] governing which outcome is recorded along an RSO trajectory. Decoherence supplies the quasi-classical alternatives, with measures given by |ci|2.

Born values are real—predictive—patterns in the RSO's observational flux. They serve as structural norms for matching instrumental credence conditional on one's present state. Relative state probability is thus prospective de se uncertainty without self‑location: a single self facing multiple decohering measurement outcomes. In this sense, the Born rule emerges in P1 for the RSO as a structurally fixed, observer‑relative measure grounded in the apodictic certainty of empirical–phenomenal experience.

Non Ab Initio RSO

From the viewpoint of the theory all elements of a superposition (all "branches") are "actual," none any more "real" than the rest.

— Everett, Letter to Bryce DeWitt, 1957 [18]

While all branches are equally real, the RSO's actual reality is disclosed in the empirical experience of its phenomenal world. This empirical–phenomenal experience is fundamentally non ab initio. The RSO never begins from an idealized, isolated state as it is always "in media res", an already entangled component of its decohering branch trajectory. This relative state reality is recorded in its P1 memory trace, and it knows its world only through this observational, correlation-inducing process. The RSO-centric view reframes the nature of branching: If the RSO is always itself an evolving superposition within P2 then branching is not an intermittent, ad hoc event triggered by lab measurements in a classical environment. Rather, branching is the continuous and fundamental nature of the evolution of the RSO's singular, empirically actual reality (P1).

What is a 'world' with respect to the non ab initio RSO? In the first instance, 'world' is defined by the quasi-classical phenomenal world disclosed in the RSO's observational flux. One can then work back from this empirically given instance of a 'world' to extrapolate 'many' worlds. Any 'world' is thus a branch trajectory through the correlation structure of ΨU, an emergent pattern of correlations that becomes stable and self-consistent for the RSO through its own environmental decoherence. In this way, a 'world' is not a static pre-existing container but an observer-centric branch trajectory that constantly arises (P1) from within the correlation structure of ΨU (P2).

Such a 'world branch trajectory' is a potentially observable universe if it allows for the evolution of a RSO. And any actually observable universe, such as ours, has a RSO to bear empirical witness to its observability. The RSO's actual world is not one of 'many worlds' but of a single, evolving branch in an observational flux of correlations. Unobservable 'worlds' are orthogonal correlations, continuously shed as environmental decoherence entangles the RSO in its singular observable branch trajectory. This world process is innately non ab initio, as the RSO is already embedded within a constantly evolving cross section of the correlation structure of ΨU, making its empirical-phenomenal world the primary world of 'many'. From this empirical view follows the epistemological and ontological primacy of the RSO and P1 as a function of P2. And how else are we to 'do' empirical science?

Decoherent Succession

Podolsky: It looks like we would have a non-denumerable infinity of worlds.

Everett: Yes.

— Conference on the Foundations of Quantum Mechanics, 1962 [11]

The model sketched in this essay maps the continuous unitary evolution of ΨU (P2) to the RSO's discrete stream of observational memory and its phenomenal experience (P1) as a singular branch trajectory. At each branching event, the RSO’s state becomes correlated with one locally stable decohering branch, while the other branches disappear into unobservable orthogonal states, effectively fading from the RSO’s empirical reality. This 'fading' is not a physical disappearance but a constant suppression of interference—the other branches becoming unobservable due to the einselection of the RSO’s state. At the next branching event, the same decoherence process repeats: the RSO’s trajectory follows one branch, while the remaining branches peel off into the wider correlation structure of ΨU. The RSO’s world is a cascading decoherent succession where only the currently correlated branch is empirically real, while past 'faded' branches persist globally but are, for all practical purposes, inaccessible.

How fast does this happen? There is no exact answer as it depends on how finely we resolve the details and on the specific environment, but for any typical RSO environment it is effectively continuous. As a roughly illustrative heuristic guide, consider Alice—after a long night in the lab—emerging to bask in the brilliance of the noonday sun. With a solar flux near 1000 W/m2—which is on the order of 1021 photons per square meter per second over about 1.5 m2 of her body—just one decohering interaction per photon would yield 1021 branching events per second. This heuristic coarse-graining of continuous unitary evolution is not a literal branch count but it indicates the 'non-denumerable' rate at which the RSO’s branch trajectory is continually updating.

So what is an observer and its observable world? From the RSO view, our phenomenal experience (P1) is co-instantiated in a stable observational flux of memory reflecting a single, constantly decohering branch trajectory along a cross section of the possibly infinite-dimensional correlation structure of ΨU (P2). And if, after all this, you are still uncertain which branch you occupy, a quick pinch should suffice to 'self-locate' your present empirical coordinates! [19]