1. Introduction

The issue of whether we make decisions freely has vexed philosophers for millennia (Kane, 2002). If we live in a world where our current actions are determined by earlier states of the world, everything we do is predetermined by cosmological initial conditions (Sapolsky, 2023). This has troubling implications. Do we absolve Hitler from moral responsibility because his genocidal actions were predestined by initial conditions over which he manifestly had no control? Many of us surely recoil in disgust at such a thought. Yet proposing indeterministic laws of physics does not resolve this dilemma: moral responsibility can neither arise if decisions are simply the result of random intra-neuronal fluctuations over which we also have no control (Harris, 2012). Having some control over our decisions seems an essential ingredient of free will.

Motivated by this, a decision-theoretic model which exploits the noisy low-energy characteristics of the brain is proposed in Section 2 and shown to be superior in a number of respects to a model based on maximising `pros minus cons'. In Section 3 we extend this model to attempt to explain not only that we have free will, but why it is such a visceral sensation for most of us. Here quantum physics rather than classical physics is shown to play a vital role. We use this to explain why current AI systems cannot not have free will - and hence why AGI may still be some way ahead. In Section 4 we discuss a possible model for a random quantum variable as a freely specifiable boundary condition to space-time at the Planck-scale interface.

A key conclusion of this essay is that whilst quantum physics is often seen as incomprehensible. Here, for once, we claim that quantum physics provides a completely intuitive commonsensical model of free will and moral responsibility, compared with the utterly bizarre logic of predestined determinism in classical physics (in which both free will and moral responsibility are denied). By way of illustration, in Section 5 we consider the dilemma of what to do had Hitler been caught alive at the end of WW2.

2. A Stochastic Model of Decision Making

The human brain is a noisy organ (Rolls and Deco, 2012). It has evolved in such a way to allow vast numbers (c. 80 billion) of extremely slender neurons to operate inside relatively small dimensions, with power requirements some 6 orders of magnitude less than a modern supercomputer but in some respects with similar data processing capabilities.

Of course, if noise had been detrimental to the operation of the brain, such low-energy miniaturisation would have been an evolutionary dead-end. But manifestly it has not been so; we are the dominant species on the planet. Why was noise not detrimental? It is broadly because in nonlinear systems (which the neural network of the brain surely is par excellence) noise can be a constructive resource and not the nuisance it is conventionally considered to be (Palmer, 2022).

An example of the use of noise as a constructive resource comes from the technique known as stochastic rounding in numerical analysis (Hopkins et al, 2020). This is used for solving complex nonlinear equations, such as the Navier-Stokes equations for climate modelling, with low-precision arithmetic and hence with relatively small expenditure of computational energy (Paxton et al., 2022). Here random numbers are used to truncate the bit length of a number Z. Suppose Z lies between Za and Zb, the two numbers which lie closest to Z in the set of numbers representable in reduced-precision format. Instead of systematically rounding to the nearest representable number, the traditional approach in numerical analysis which can lead to an undesirable accumulation of round-off error, Z is rounded to Za with probability

and to Zb with probability

Hence, when Z is close to Za or Zb, the noise has little impact and it is very likely that Z will be rounded to Za or Zb respectively. However, when Z is equidistant between Za and Zb, then the noise has maximal impact and it is as likely that Z will be rounded to Za as to Zb. Hence C is a parameter which controls the impact of the noise in the numerical solution. An example of stochastic rounding is illustrated in the figure below.

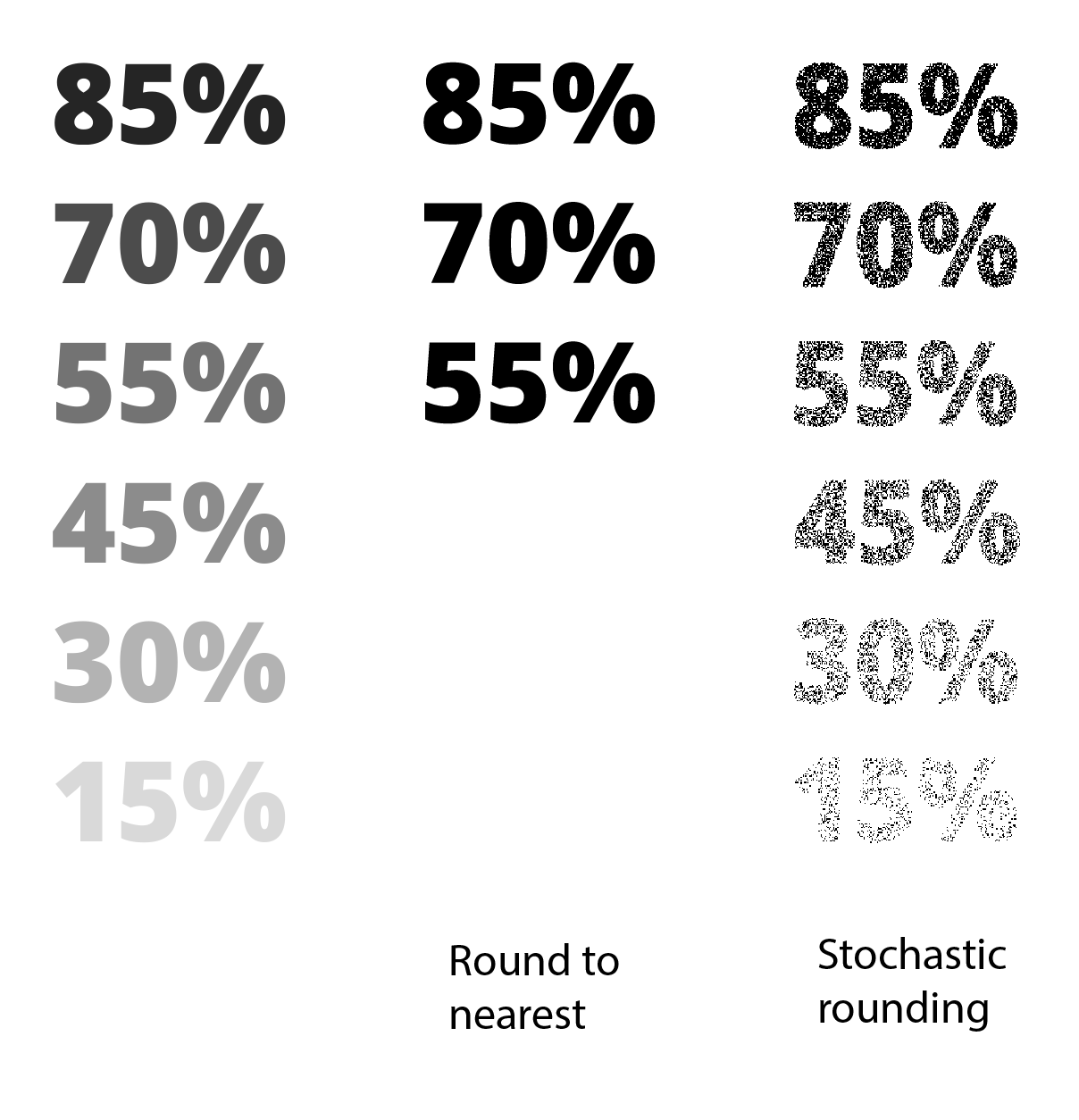
Figure 1. On the left, the percentage figures are shown in different shades of grey. In the middle the figures are rounded to one bit in a systematic round-to-nearest way. On the right the pixels in the figures are also rounded to one bit, but using the stochastic rounding technique. Hence, for example, there is a 0.3 probability of rounding to the black pixel in the 30% figure. Clearly more information survives the truncation with stochastic rounding compared with round to nearest.

Here we apply the stochastic-rounding strategy to human decision making. Many of us attempt to make decisions by weighing up the pros and cons of each option and deciding on the one where the pros minus cons is largest. The problem is that pros and cons are typically not comparable, and trying to compute an elusive maximum can lead to the classic `paralysis by analysis' which prevents a decision being made at all. This is evolutionarily disadvantageous - carefully weighing up the pros and cons of multiple escape routes could prove fatal when being attacked by a predator.

To apply stochastic rounding to decision making, imagine a series of decisions, each with 2 options: 0 and 1. Here Xn, equal to 0 or 1, is the nth decision and Yn, lying strictly between 0 and 1, is a random-number input to the decision procedure

a function of the control variable Cn lying strictly between 0 and 1, such that the probability that Xn=1 is equal to Cn. An explicit mathematical model for such a function is provided in the Technical Endnote. Like stochastic rounding, if Cn equals 0 or 1, the decision is certain (Xn=0 or 1 respectively) and independent of Yn. If Cn=1/2, the decision depends entirely on Yn. For other values, Cn provides partial control over the impact of the random input Yn.

In terms of the brain, we may suppose a default value Cn=1/2 (though genetic preconditioning may bias Cn away from this default). Deviations from the default value are determined by past memories and experiences. But it takes energy to draw on these past experiences and thus deviate from the default. Energy is a valuable resource for biological systems. Therefore we should only draw on these past experiences and deviate from the default when we need to. An important principle when considering biological mechanisms, is that biological systems typically appear to have evolved to use energy extremely efficiently.

Let us compare a stochastic-rounding decision strategy with a deterministic round-to-nearest decision strategy (comparable to weighing up pros and cons and choosing the biggest) where

is the integer closest to Cn. There are a number of advantages to stochastic rounding over round-to-nearest. The first is directly related to the accumulation of round-off error in numerical analysis. If we always round to nearest then we will systematically opt for an irrationally risk-averse strategy; we will never decide to pursue the 1 option if Cn is less than 1/2 (even slightly). However, one of the key reasons why humans have thrived as a species is by not being so pathologically risk averse. Perhaps our noisy brain has helped us become the dominant species on the planet. A second advantage of the stochastic-rounding strategy is that instantaneous decisions can always be made with the default Cn=1/2: paralysis by analysis need never occur. A third advantage is that stochastic rounding is an energy-efficient strategy. The vast majority of decisions we make every day (perhaps what clothes to wear in the morning, what to each for lunch) are relatively unimportant and can be executed with a low-energy Cn =1/2. In this way, we don't waste valuable energy making decisions.

As small children with few past experiences to fall back on, we default to Cn=1/2 (though genetic preconditioning can preset other values). However, a bad experience can lead to a rapid update in Cn, e.g. when next deciding whether to dip one's hand into a bowl of steaming water. At the other end of life, many of us get `set in our ways' as we get older, so that Cn naturally tends to either 0 or 1 as n becomes large. We make less use of the noisy resource the brain has given us for decision making, anguish more and more over small and unimportant decisions, and generally become more and more risk averse. Perhaps as a consequence our creativity wains (Palmer, 2022).

3. Free Will

Below, we consider free will from two perspectives: as being able to have done otherwise, and as a very visceral sensation. We argue that both of these require the decision-theoretic model described above to be based on quantum mechanical principles and not classical principles. A major conclusion of this essay is that when we do this, the physical basis for free will and moral responsibility becomes intuitive and commonsensical. This is one example, where, by contrast, classical physics, based on predestined determinism, seems unnatural and for the author at least, incomprehensible.

At face value it is not unreasonable that the stochastic rounding model should have a quantum basis, since the impact of randomness in a quantum mechanical measurement is structurally similar to the stochastic-rounding model above. For example, consider a spin-1/2 quantum particle prepared spin up with respect to a fiducial direction and then measured at an angle

to the fiducial direction. Here the measured outcome Xn (0=down, 1=up) can be represented by our decision rule above, where, from Born's Rule, the experimenter-controlled quantum probability

can be identified with the control variable Cn and where Yn is a `genuinely random' (Bierhorst et al, 2023} quantum variable (see also Section 4). For example,

and it is certain that the output is 0 or 1 respectively. Similarly

and the output is equally likely to be 0 or 1. This gives us some support for supposing that the proposed stochastic-rounding model might be realised in terms of quantum physics and that Qn=Cn. Other reasons for drawing such a conclusion are discussed in the next sub-sections.

The primary reason the brain operates on the principles of quantum physics may have nothing to do with free will, but rather that quantum processes in the brain can be much more energy efficient that corresponding classical processes. An example is the transport of ions across ion channels in the membrane of a neuron Summhammer et al (2018) where quantum tunelling makes for a much more energy efficient transport process. In so far as free will emerged from such primitive energetic considerations, it was clearly evolutionarily advantageous for it to do so.

3a Counterfactuality

For now, let us define free will in the way it is often defined in abstract philosophical discussions - in terms of an ability to have done otherwise (Kane, 2002). Later we will consider free will in more physical terms.

Since the experiences that determine Cn have occurred in the past, or have been genetically predetermined, then we will presume these as fixed and unchangeable. The critical question then is this: could Yn have been otherwise? If Yn was generated by a classical deterministic pseudo-random number generator, then we can think of Yn as the output of a machine/algorithm which itself has an input. If we seek a change in the output Yn then we must seek a change in the input event En. But En is in turn affected by events in its causal past. Hence, we are back to predestination: in a classical world, asking whether Yn could have been otherwise is tantamount to asking for a completely different set of cosmic initial conditions. As with the events determining Cn, we consider cosmic initial conditions as fixed and unchangeable. From this classical point of view, it does not make sense to ask whether we could have done otherwise.

However, in quantum mechanics we think of quantum noise as truly random (Bierhorst,2023). But what does this mean? In his important paper Free Variables and Local Causality Bell (1985), focusses attention on a theory's free variables: ones that by definition can be altered keeping other variables in the theory fixed. In quantum physics we should think of Yn as a free variable. If Yn is a free variable, it could have been otherwise at times earlier than tn when its value was set. Hence our decisions could also have been otherwise for times earlier than tn. In Section 4 we discuss a physically based model of a free quantum variable in terms of a freely specifiable boundary condition to space-time at the Planck-scale interface. From this perspective, we can conclude that we could have done otherwise if the source of noise for our stochastic-rounding model of decision making is quantum rather than classical noise. The only time when we don't have free will is when we are absolutely certain how we will decide (so that Cn=0 or 1 and Xn is independent of Yn). Like Luther at the Diet of Worms, when Cn=0 or 1, here we stand and can do no other (Dennett, 2012).

3b The Visceral Sensation of Free Will

We focus here on the more important visceral sense of free will that most of us experience routinely when we make decisions. It's not simply that we could have done otherwise, we feel that we could have done otherwise very keenly (so keenly that we might admonish ourselves for weeks, months, years, even for the rest of our lives, if we made what we felt was a bad decision). Would an AI system admonish itself in this way? If not, why not?

The state-space trajectory associated with a classical system is a 1-dimensional curve, even if the position of this trajectory in state space

is uncertain. By contrast, in quantum mechanics, the quantum state is a (phase-weighted) integral over all possible classical paths. (Because of interference, it is enough to consider the quantum state as a sum over paths close to the classical path.) From this we can deduce that the quantum state is drawn from multiple state-space trajectories and not a single trajectory as in classical physics. Deutsch (1989), one of the founding fathers of quantum computing, concludes that such quantum parallelism is the key resource that gives quantum computing its advantage over classical computing. We take such a view here too.

But the brain is not a quantum computer in the normal sense of the word - decoherence times are too fast in the warm noisy brain for us to be able to factor large integers for example. However, there may still be vestiges of quantum parallelism in our cognitive capabilities. Here it is suggested that a vestigial awareness of the quantum parallelism over which the wavefunction is summed during decision making explains the visceral feeling that we are free in making decisions.

That is to say, if decision making draws on quantum physics, and quantum parallelism in particular, then we will have a cognitive awareness of the counterfactual worlds associated with making different decisions, not through signals from our sensory organs, nor from approximate 'pro minus con' calculations that we may or may not do, but from the direct projection of the quantum state onto the neuronal state of the brain. The key point is that this cognitive sensation, if it is generated by the effects of quantum parallelism, is a real physical experience and not merely the consequence of having emulated some counterfactual world by an approximate computational procedure.

Such cognitive sensations are necessarily fleeting as quantum coherence times are so short in the brain (Tegmark, 2000). One can perhaps relate such experiences to those of looking at photos on a smartphone, where we are shown videos for the first fraction of a second after the photos are displayed. The fleeting image of motion somehow provides an enhanced sense of reality to the photo which persists after the video has finished. Similarly, fleeting moments of quantum coherence may provide us with that hard-to-pin-down sense of reality that somehow transcends mere perceptual data input.

3c Moral Responsibility and AI

As discussed in the Introduction, it is impossible to attribute a sense of moral responsibility to decisions if they are predestined by cosmological initial conditions or equally if they are the result of unfettered (i.e., uncontrolled) randomness. In the context of the stochastic-rounding model of decision making, it is therefore impossible to attribute a sense of moral responsibility to decisions made where Cn is equal to 0, 1/2 or 1. Hence, a necessary condition for having a sense of moral responsibility is partial input to decision making from our past experiences, and partial input from stochasticity.

But this is hardly a sufficient condition. An AI system could be encoded with the stochastic-rounding model described in the Supplementary Information using classical pseudo-random numbers for noise. According to the discussion in Section 3a, the AI system could not have done otherwise. But this is surely too metaphysical a property to rule out AI free will in any practical sense. So in what practical sense does the AI system fail to have a property of decision making that we humans have? It surely relates to this physical cognitive awareness of the counterfactual worlds we choose from when making a decision, as discussed in Section 3b. An AI system based on classical physics and pseudo-random numbers cannot have such a cognitive awareness by construction.

At exactly what stage of sophistication an animal brain starts to have this sense of self-awareness is unclear. For example, merely replacing a classical source of noise with a quantum source of noise (but keeping everything else classical) would not be enough to provide a brain with the type of cognitive awareness discussed. One can imagine that there is no hard boundary between brains with free will and brains without. For this reason, we cannot rule out the possibility, indeed likelihood, that non-human animals have a sense of free will too. But this is surely as far as we can go without understanding more about the quantum nature of the brain.

Self-awareness about decisions made, provides the basis for having a sense of moral responsibility: we literally `knew what we were doing' when we decided to do something. In this sense, free will, moral responsibility, consciousness and even creativity appear to be highly interlinked concepts.

Perhaps in future years we will build AI systems based on quantum physics, but it will likely take some time. For that reason, we must be sceptical about claims of AGI in near-future AI.

4. Free Variables at the Planck-Scale Interface

Our model of free will depends on Yn being a free variable, one that could have been otherwise, the rest of the universe being unchanged. But what does this mean? Here we give a possible physical example, again exploiting the concept of nonlinearity.

Consider a nonlinear system where information cascades upscale from small to large scales, e.g. as represented by the shift map

A simple and extremely pertinent physical example is a system of colliding billiard balls. Such is the power of exponential growth in chaos theory, after a mere 17 collisions the macroscopic position of a billiard ball on the billiard table is rendered completely uncertain by an initial uncertainty in the position of the cue ball by a single Planck length (Raymond, 1967; Berry, 1988). On the other hand, from the uncertainty principle, the energy required to probe Planck-scale fluctuations is so large that any measuring system capable of so doing will self-collapse into a black hole (hiding any relevant information from us). Sub-Planck scales are thererore inherently unknowable.

Hence one way of interpreting Yn as a free variable - one that invokes both quantum and gravitational effects - is if its value is determined by an inherently unknowable boundary condition to space-time at the Planck scale, the information from which propagates upscale e.g., by the shift map above. That is to say, let us simply assume sub-Planck scales do not exist and the impact of Planck-scale information on space-time is determined by a boundary condition to space-time at the Planck scale, and a nonlinear propagation equation, and not by an initial condition as in classical physics. See Fig 2. We won't pursue this idea further here, but it provides a way of thinking about free variables which, as Fig 2 suggests, is fundamentally different to those of classical pseudo-random variables initialised at the time of the Big Bang.

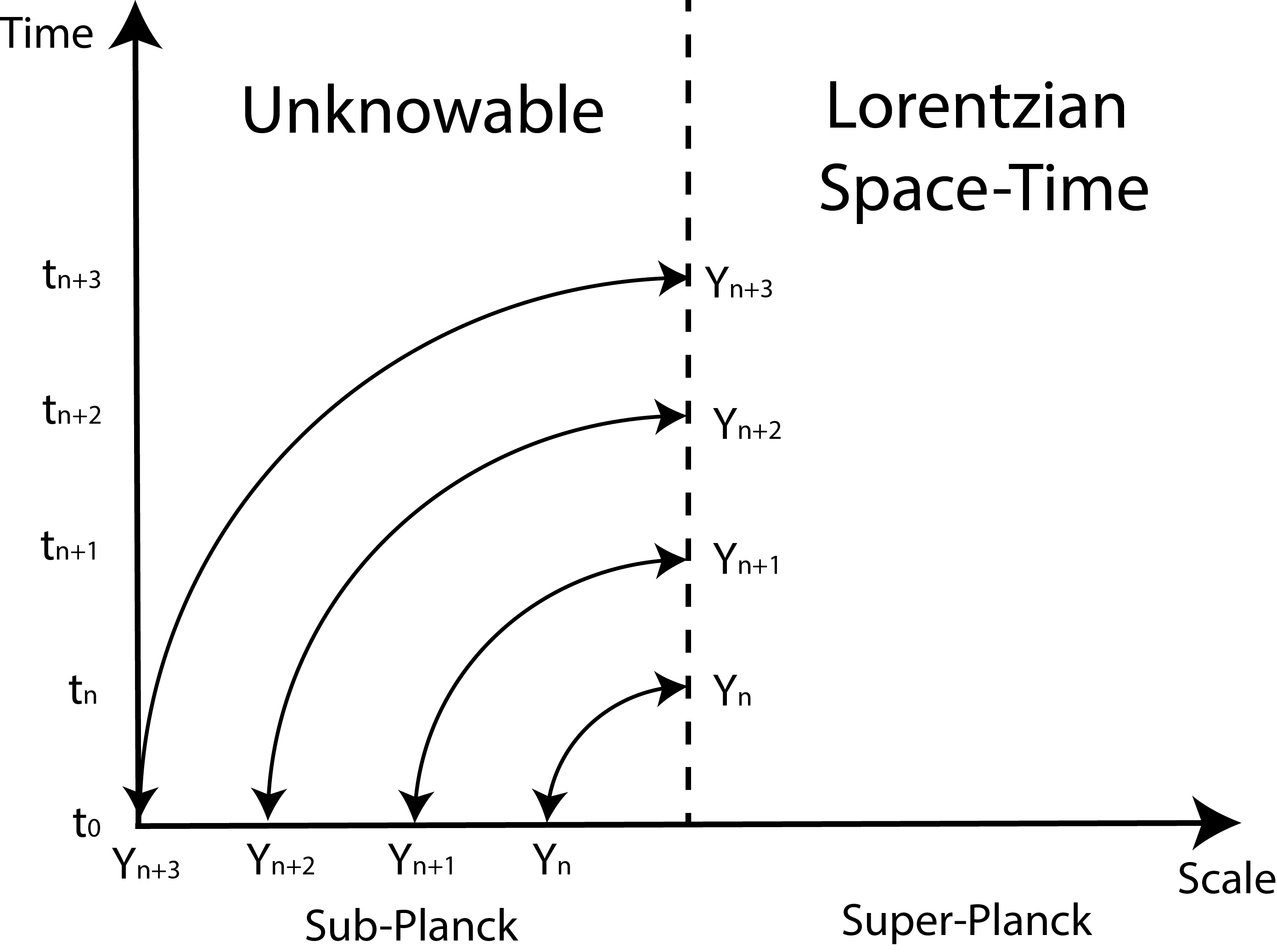
Figure 2. Variables Yn that classically would be considered part of the cosmological initial conditions, and therefore fixed and unchangeable at all later times, can instead be considered as unknowable freely-specifiable boundary conditions at the Planck-scale interface to space-time, injected into space time at times tn and propagated upscale by nonlinear dynamics. That is to say, we simply assume sub-Planck scales do not exist and the impact of Planck-scale information on space-time is determined by a boundary condition, and not an initial condition. For all practical purposes this boundary condition appears truly random. In this picture, before tn, Yn is undetermined in space-time, and therefore could have been otherwise. It is a free variable in the sense of Bell (1985).

5. Conclusions

We have devoloped a model of free will based on ideas from classical numerical analysis, but where quantum physics was shown to necessarily play a vital role. Quantum physics is usually thought of as counterintuitive, even incomprehensible. Here, for once, invoking the principles of quantum physics provides us with a completely intuitive and commonsensical model of free will and hence moral responsibility, in comparison with the utterly bizarre logic of classical predestination where both is denied.

By way of illustration, let us return to the example of Hitler, mentioned in the Introduction. Suppose Hitler had been caught alive at the end of WW2. Should he have been executed for his crimes? It is argued by those who believe in predestination that punishment should not be given in retribution for a crime, but simply as a deterrent to stop both the criminal themselves from reoffending - and others tempted to commit a similar crime - and keeping a dangerous individual off the streets (Sapolsky, 2023}.

According to this logic, there would be no reason to execute Hitler. He was an ill man at the end of WW2 and there was very little prospect of him getting back to power and reoffending. And genocide is such a singularly perverse crime against humanity that executing Hitler is hardly likely to deter future genocidal maniacs. Indeed, perhaps such individuals may welcome the prospect of being executed in order to achieve some kind of martyr status amongst followers. On this basis, those who believe in predestination might argue that it would have been enough to put Hitler under house arrest (as Napoleon was, on St Helena) for the remaining months or years of his life. But most of us would be outraged by such an inconsequential punishment, given the millions Hitler murdered. Following the quantum analysis in this paper, Hitler was clearly morally responsible for his decisions, classical predestination notwithstanding, and should have been punished accordingly.

This, for most of us, is just common sense. Considered the right way, perhaps all of quantum physics will turn out to be simply common sense.

Technical Endnote

We seek a functional relationship

where Yn is a stochastic variable lying strictly between 0 and I and comprising N independent bits, i.e. Yn=0.abc... d where each bit a, b, c,...d is independently equal to 0 or 1 with probability P=1/2, and Xn = 0 or 1 such that

Consider the case N=3. With Yn=.abc it can readily be checked that

where a' denotes the bit complement of a etc. Hence, if

and we define

then indeed P(Xn=1)=Cn. This is straightforwardly generalised for arbitrary N.