
Adam Brown
Forget the cat: what if you put a computer into the Schr枚dinger thought experiment? You could make the computer both run and not run, at once, and that's just a warm-up. You could, in fact, make it not run and nonetheless extract the answer to a computation. The computer will be sitting there waiting for someone to press "Run," yet will have produced a result. It sounds impossible by definition, but that's quantum physics for you. This idea of counterfactual computation is not just a thought experiment; there are computers in the physics labs of the world that have done this.
At the recently concluded FQXi meeting in Tuscany, Adam Brown of Stanford University grabbed hold of counterfactual computation and ran with it. What if the computer is set up to perform a brain simulation? You could ascertain what that brain would be thinking even if it is not, in fact, thinking. Whether a simulated brain is conscious is a contentious question, but suppose it is. Then you could create a mind that acts in the world, yet lacks first-person experience--a philosophical zombie. What is more, you can decide the circumstances under which the mind will be conscious or not; it might revel in happy sensations, but have no experience of sad ones. Brown's talk put a new spin on old problems in the philosophy of mind and personal identity.
September 8, 2019
Quantum Mind Reading. Could we create a quantum experiment to predict what a person will do, without having to simulate their consciousness? Physicist Adam Brown argues a classic quantum "bomb tester" proposed in the 1990s could be modified to do just that.
Full Podcast
Of all the many wonderful talks I've heard at these meetings over the years, Brown's stands out as one of the most quintessentially FQXi: uninhibited and unpigeonholeable, less about the conclusion than about the steps leading up to it. "I am not really a quantum information theorist, and I'm really not a philosopher," he admitted at the outset. "But what I am is amongst friends, so I hope you will take this in that spirit."
Speaking of being amongst friends, let me put out a general-purpose disclaimer of my own. In this post, I will streamline the experimental descriptions, departing slightly from the authors' original presentations, while staying true to the physics. Also, I will steer clear of the interpretation of quantum mechanics and focus on what we directly observe in these experiments. We will have plenty of interpreting to do as it is.
Please Do Interfere
Counterfactual computing is nothing so straightforward as predicting what the computer's output will be. It's not like saying that you know the computer would beep if you pressed a key, but you don't press that key. In fact, the machine's output could be unpredictable and, under ordinary circumstances, the only way to know what it will do is to run it. Yet quantum physics can obtain a prediction even so. It works because, in the quantum realm, things that can happen, but don't, can leave their mark on what does.
The principle of doing something without doing it goes back to the earliest days of quantum theory. Physicists came up with ways to measure a particle without interacting with it (the Einstein-Podolsky-Rosen thought experiment), to affect a charged particle without exerting any force on it (the Aharonov-Bohm effect), and to collapse a wavefunction without measuring it (the Renninger negative-result experiment). Tellingly, these authors were critics of the Copenhagen interpretation of quantum mechanics. They were after features of the theory that challenged the conventional wisdom.
The specific idea of counterfactual computation grew out of a proposal in 1991 by Avshalom Elitzur and Lev Vaidman, both then at Tel Aviv University. They suggested creating a superposition of two possibilities, then un-creating it, which should restore the initial state--unless something happened in the interim to either of the superposed possibilities. Even if something could have happened, but didn't, it will prevent you from reconstituting the original.
Their proposed experiment uses a quantum interferometer. You fire particles at a beamsplitter, which directs them randomly one way or the other. For photons, a half-silvered mirror does the trick; half reflect off and half pass through. Or you also glue two triangular prisms together to form a little cube; half the photons will leave through one face and half through another. The two paths diverge and meet again at a second beamsplitter. That beamsplitter, likewise, directs the particles one way or another, where detectors await them.

Credit: Adam Brown
Even before you introduce a counterfactual, this setup violates classical intuitions. If beamsplitters were simply gates that shunted particles either left or right, half would land in one detector, half in the other. What we observe, though, is that all land in one detector. That means the first beamsplitter must be causing each particle to go both left and right--a superposition of the two paths. When the two paths meet at the second beamsplitter, they interfere with each other, which closes off one of the directions the particle might have taken. So, the second beamsplitter reverses the operation of the first: if the first splits one particle in two, the second combines two into one.
The fun begins when you stick an obstacle into one of the two paths. Then the two paths no longer meet at the second beamsplitter. No interference occurs. Now the first beamsplitter does act like a simple gate, sending particles just one way or the other at random. Half the time, neither detector clicks--the particle must have gone down the blocked path. The other half, one of the two detectors clicks, at random--the particle has evidently reached the second beamsplitter and been steered to one of the detectors.
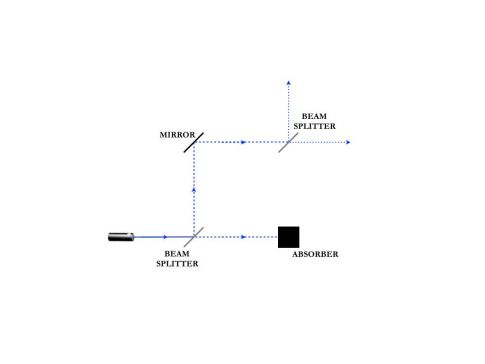
Credit: Adam Brown
The upshot is that, if the quiet detector starts to click, you know that someone has inserted an obstacle into the system. The converse is not true: if the normally active detector goes off, there might or might not be a blockage. This system thus acts as an obstacle-detector. What is counterfactual about it is that the particle was supposed to be blocked, but there it is, exiting the apparatus. The only effect of the obstacle has been to alter its exit point. Evidently the particle must not, in fact, have hit the obstacle, but nonetheless felt its presence.
As with much else in quantum physics, the core weirdness is the uneasy mix of particle and wave behavior. Without the blockage, the photon acts like a wave. It divides at the first beamsplitter and reunites at the second, like an ocean wave parting around an island. With the blockage, it's like a particle, delivering all its energy in one lump. The counterfactual detection of the obstacle leverages this duality. Elitzur and Vaidman described this as an instance of quantum nonlocality: the presence of an obstacle affects the output not by any mechanistic process that you can trace out step by step, but by the sensitivity of the output to the system in its entirety.
Bomb Squad
Elitzur and Vaidman put the blowing into mind-blowing by imagining a hair-trigger bomb as the obstacle. If so much as a single particle falls on this bomb, it detonates. If someone opposing your tenure case plants such a bomb in your apparatus, you will hear one of two things when you perform the experiment: a loud bang, or a gentle click from the normally inactive detector. If the latter, the instrument will have detected the bomb without interacting with it--an otherwise impossible feat.
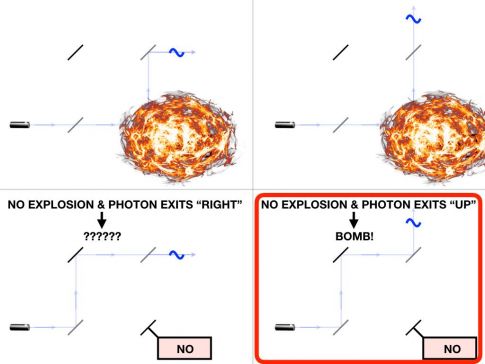
Credit: Adam Brown
Clever though this bomb-sniffer may be, please don't trust your life with it. Because the beamsplitters divide their beams evenly, the system will set off the bomb half the time; the other half, it will reveal the bomb with only 50-percent likelihood. In all, it has only a one-in-three chance of giving you advance warning. You can do better by modifying the beamsplitters to send fewer particles down the pathway that might contain a bomb, which reduces the probability of an explosion. The tradeoff is that it also also reduces the probability of a safe detection. Favoring one path over the other weakens the interference effect at the second beamsplitter, and some particles will leak through to the normally inactive detector. You will get false positives, suggesting the presence of a bomb where there is none. Put simply, if you avoid an explosion by not bothering to look, you are none the wiser about whether a bomb is there.
But Paul Kwiat of the University of Illinois at Urbana-Champaign and his colleagues came up with a way to evade this tradeoff. It makes use of the so-called quantum Zeno effect, which, in this case, simply means running the check multiple times. Each time, the system adjusts the probability of sending a particle down the potentially bomb-ridden path. On its first attempt, it tries a very low probability. If a bomb lurks in the system, it will probably not detonate, but its presence nonetheless prevents interference from occurring at the second beamsplitter. If the system is bomb-free, interference does occur, but only weakly.
To create a cleaner distinction, the particles loop back for another pass through the apparatus. Based on the results of the first round, the system adjusts the probability of sending particles down the potentially bomb-ridden path. If it sensed even the whiff of interference, suggesting the path is clear, it nudges the probability up; otherwise, it keeps the probability low. If a bomb is present, it is no likelier to detonate than before, but if it isn't, the interference is somewhat stronger. Crucially, the system can make these adjustments using passive optical elements, without detecting the photons, which would spoil the interference rather than amplify it.
After enough rounds, the system has shifted from sending few particles down the potentially bomb-ridden path to sending all of them, having ascertained that there is no risk of explosion. At this point, the bomb and bombless states are completely distinct, avoiding false positives. Only then do you steer the particles into the detectors to see which of those states the system is in.
An entertaining noir film about the bomb tester, created by Dag Kaszlikowski of the Centre for Quantum Technologies and set on the mean streets of Singapore, won the 2014 FQXi video contest.
[youtube:I7oZAo8hJnU, 560, 315]
Kwiat and his colleagues wrote up a Scientific American article in 1996 that clarifies the procedure.
Seeing in the Dark
Once you realize that you can interact without interacting, all manners of possibilities open up. Kwiat and his colleagues used the scheme to take microscope images of hairs, wires, and fibers without shining light on them (Physical Review A 58, 605-608, arXiv:quant-ph/9803060 (1998)). Vaidman suggested that biologists could take x-ray images of cells without causing radiation damage arXiv:quant-ph/9610033 (1996). Jian-Wei Pan of the University of Science and Technology of China and colleagues transmitted an image using hardly any photons. Roger Penrose of Oxford, in Shadows of the Mind, puckishly suggested that Orthodox Jews could use the system on the Sabbath to turn on a light without touching its switch.
In one especially interesting variant, Lucien Hardy of the Perimeter Institute showed how the bomb itself could be placed into superposition (Phys. Rev. Lett. 68, 2981 (1992)). He added a second interferometer that contained an antiparticle. It overlapped the first interferometer, so that the antiparticle could meet the particle and annihilate it in a minor explosion. Hardy originally imagined using electrons and positrons, but experimental demonstrations have used photons, which wipe each other out not by particle-antiparticle annihilation, but by mutual negation in a beamsplitter (Phys. Rev. Lett. 95, 030401 (2005)) or nonlinear optical crystal (Phys.Rev.Lett.102:020404 (2009)). On occasion, the normally inactive detectors of both interferometers click, indicating that an annihilation took place--but if it did, how did particles manage to reach the detectors? The scenario came to be known as "Hardy's paradox," although Hardy did not use the word "paradox" himself. A paradox arises only if you suppose the particles must always have well-defined positions.
Counterfactual Computing
In the most astounding proposal of all, Richard Jozsa of Cambridge proposed in 1998 that you could swap the bomb for a computer (arXiv:quant-ph/9805086 (1998)). The particle is its on/off switch. Just as you can detect a bomb without interacting with it, you can obtain the output of the computer without running it.
Jozsa imagined a rudimentary computer that outputs a single bit. A value of 0 is like the absence of a bomb; an output of 1 is like the presence. If the normally inactive detector clicks, the output must be 1--and the computer has yielded a result even though it wasn't run. You can confirm that by looking at the machine. It will still be in its initial state, never having performed the computation. Yet its mere presence skewed the interferometer.
Like the bomb tester, this system often produces ambiguous results. You can do a bit better by augmenting it with the Zeno procedure.You set the probability of running the computer low at first and, as long as its output remains 0, gradually ratchet up that probability. By the end, an output of 1 is unambiguously a counterfactual output. Even that isn't perfect, though. If the result of the computation is 0, the computer will run. There's no way to perform a computation that is counterfactual no matter what the output is. In a follow-up paper, Jozsa and Graeme Mitchison of the Laboratory of Molecular Biology in Cambridge showed that this tradeoff is unavoidable. A counterfactual computer can never deliver complete certainty about both output values because its very functioning depends on uncertainty: that it might or might not run.
Kwiat and his team built such a machine in 2006 (Nature聽439, 949-952 (2006)). Their computer returned two bits, indicating which of a set of four items met some criterion, using a famous algorithm developed by Lov Grover. The researchers placed it into one path of an interferometer. Running this computer is like exploding the bomb: it absorbs the particle, neither detector clicks, and you have to read the output from the machine itself.
The system produced one of three outcomes. Half the time, neither of the interferometer detectors clicked, meaning the computer ran. The counterfactual aspect failed in these cases, but at least the team had a very nice implementation of Grover's algorithm (the best to date). A quarter of the time, the normally active detector clicked, which told them nothing: the computer may or may not have run. The remaining quarter, the normally inactive detector clicked, indicating that the computer did not run, but nonetheless gave a partial output. The researchers proposed stringing together a series of such interferometers to extract the rest of the output.
So what's it good for? Josza suggested that counterfactual computation was yet another odd effect that quantum computers might someday harness, and Kwiat and his colleagues suggested that it might be adapted to reduce the errors that quantum computers are prone to. These uses are far off, at best. Brown, in his talk at the FQXi meeting, offered a more immediate application: for philosophy.
A New Breed of Zombie
Brown聽connected counterfactual computation to philosophical puzzles having to do with the mind. "There is, in fact, a reason you should care about whether the computation happened or not, and that's if what the computation is doing is simulating your thought process," he said.
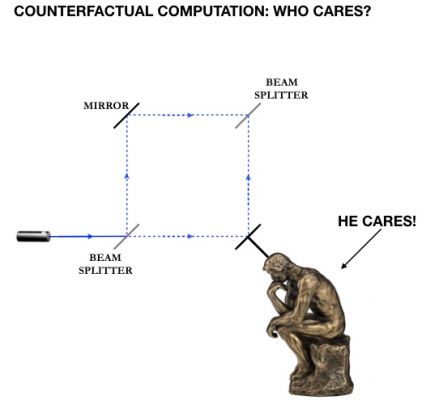
Credit: Adam Brown
Suppose you program a computer to simulate a conscious mind. By putting this computer into an interferometer, you can predict what the mind will do without running the simulation. "Using counterfactual cognition, you can simulate what somebody's going to do--you can predict what they're going to do--without simulating them," Brown said.
"Predict" is perhaps too weak a word. A simulated mind is a mind in its own right. You are not just predicting what the mind will do, but letting it do it. If you ask it to add 2 and 2, it will respond as readily as the original. Many philosophers and neuroscientists think a simulated mind is as conscious as the original--that is the premise of many a Black Mirror episode.
From the outside, the counterfactual mind seems identical to the original or simulated mind. Its output is the same. From the inside, though, the difference is profound. The counterfactual mind doesn't have an inside. It is a philosophical zombie. In the taxonomy of zombies, it is even weirder than other breeds, because not only is it not conscious, it doesn't even exist. It remains a potentiality inside the computer, awaiting an "on" signal that never came.
I don't think this principle is limited to computer simulations. Why not insert an actual living brain into the interferometer and use the particle to control its state of consciousness? That would bypass the controversial question of whether a simulation has the same experience as the original. If the brain's nerve connections to the body are preserved, it might move an arm without going through conscious deliberation. The brain will sometimes be fully present and sometimes a zombie.
You do run into the tradeoff that Mitchison and Jozsa talked about: not all results can be obtained counterfactually, so the mind will sometimes run and sometimes not. But Brown--in what was the most remarkable part of an already remarkable talk--made a virtue of this defect. Suppose you are simulating a mind that is making some big life decision. Such decisions are hard; with all the variables involved, you can never be sure which choice will make you happy or sad. But you can arrange the counterfactual procedure to execute only the happy outcomes and leave the sad ones unimplemented. Thus you could guarantee that any minds you conjure up will be happy. Indeed, you could apply that insight to an entire virtual universe, so that only universes that maximize the happiness of their occupants (or some other desirable outcome) were brought into existence.
Brown speculated that such a scenario bears on the problem of evil in theology. Even an omniscient creator faces a problem of prediction. If it wants to create a universe where good outweighs evil, it must, in effect, run a simulation first. But such a simulation is a universe in its own right. It seems the creator cannot avoid creating creatures that suffer. But counterfactual creation allows God to create a universe where good is guaranteed to outweigh evil.
These teleological outcomes can occur even at a more humble level. The conditions a physicist imposes at the end of an experiment can determine what happened during the experiment or whether the experiment is even performed. You can ensure that outcomes you don't like never came to pass. "If you weren't going to get the answer you didn't like, then, in a wavefunction-weighted Born sense, you never instantiated that possibility to being with," Brown said. That might have practical significance. When evaluating the efficiency of a quantum algorithm, researchers typically count how many times the computer performs certain operations, and Brown suggested they shoudn't count operations that never occur.
If nothing else, I think Brown's talk proves that physicists still have much thinking to do about quantum counterfactuality. If the potential and the actual blur together, perhaps you should conclude not that you haven't run the computer, but that, by prepping the computer, you have run it--that there is no difference between running and not running, and computation is the structure of the machine, not it its dynamics.
One thing is clear: there is nothing counterfactual about how amazing quantum physics can be.