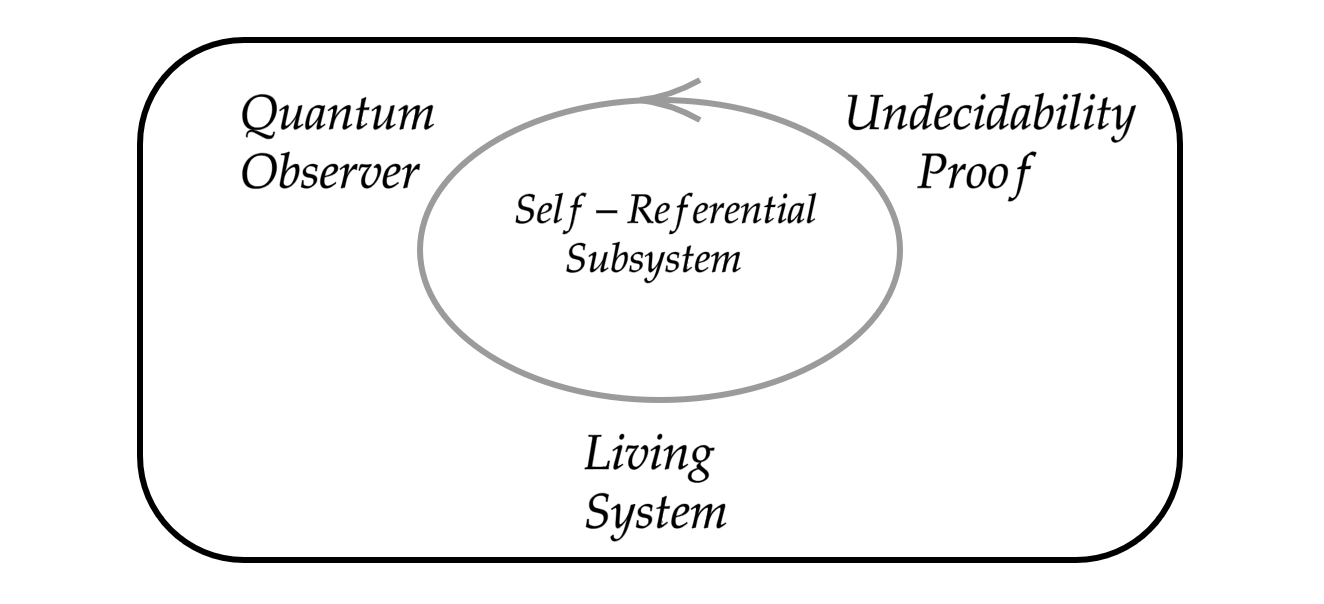
Does a complete description of biological systems require quantum mechanics? To answer Schrödinger’s question ”What is Life?”, we will consider the process of quantum measurement as a self-referential subsystem first conjectured by John Archibald Wheeler. He believed observers to be connected to the undecidability proofs of Gödel and Turing, where a no self-referential algorithm implies no generalized algorithm for some problems, like the halting problem. The three-way relation between undecidability, quantum and theoretical biology will shed light on each of the other topics. We will look at the central role of the delayed choice experiment for this framework of life—not only as the logical foundation but chronological origin. We compare this to overarching themes found in the work of Humberto Maturana, Francisco Varela, Robert Rosen, Tibor Ganti and Stuart Kauffman.
Erwin Schrödinger in his lectures "What is Life?" conjectured that there were laws of physics yet to be discovered that would explain living systems.
...living matter, while not eluding the "laws of physics" as established up to date, is likely to involve "other laws of physics" hitherto unknown, which however, once they have been revealed, will form just as integral a part of science as the former.
Leaving clues, Schrödinger brought attention to what he called "negative entropy", which has led physicists like Paul Davies, to look into the role of information and information processing in living systems. Davies has specifically emphasized the importance of functional or semantic information in living systems. For example a certain DNA sequence is more than the sum of the letters ATGC; they are orders for how a living organism ought to function. Biologist Paul Nurse has also pointed towards information and information processing as key to understanding life. Biologists speak in terms of the flow of information in terms like: genetic code, replication, transcription, translation, messenger RNA, transfer RNA, etc.
Schrödinger, who was also one of the founders of quantum theory, hinted at a future role that quantum theory may play in understanding biology. Indeed a collection of problems and methodologies under the categorization of "quantum biology" has started to blossom. Quantum biology has been used to explore avian navigation, photosynthesis and even olfaction. What if quantum theory has the key to understanding what living systems are, in the most fundamental sense? But what could the crystalline formalism of quantum theory with linear operators, eigenvectors and eigenvalues tell us about the baroque world of biology?
What if both information and information processing are necessary in a self-referential framework that is unique to what we call "living systems"? What could this have to do with the foundations of quantum theory? We will explore links between mathematical biology, quantum physics, and theoretical computer science. The field of cybernetics has much overlap with the following discussion.
The celebrated mathematical physicist Ed Witten, in a 2017 interview with Quanta Magazine noted a large gap in our knowledge of quantum theory. He stated:
When I was a beginning grad student, they had a series of lectures by faculty members to the new students about theoretical research, and one of the people who gave such a lecture was Wheeler. He drew a picture on the blackboard of the universe visualized as an eye looking at itself. I had no idea what he was talking about. It’s obvious to me in hindsight that he was explaining what it meant to talk about quantum mechanics when the observer is part of the quantum system. I imagine there is something we don’t understand about that.
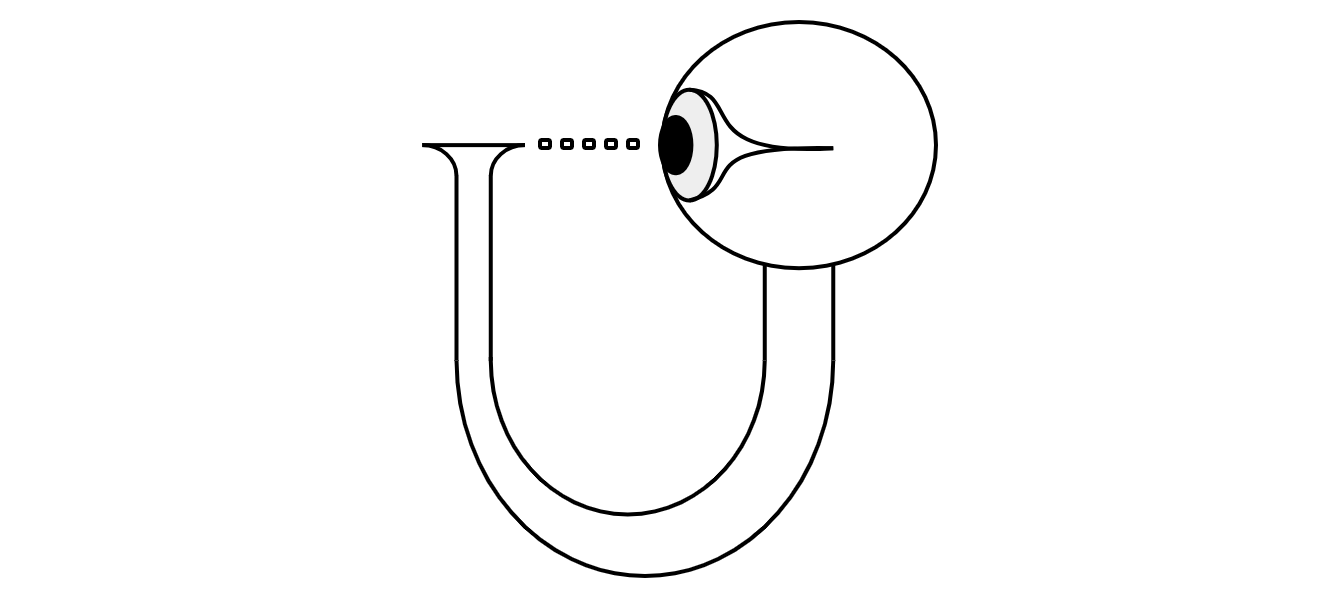
John Archibald Wheeler, in his unpublished notebooks---which are housed at the American Philosophical Society in Philadelphia--- scribbled his famous "U"-diagram throughout his notebooks over several decades (The capital letter "U" standing for "universe"). The eye observes the quantum universe that it is a part of. The eye is a self-referential subsystem, whether one wishes to call it an "observer" or "measurement".
Also in Wheeler's leather-bound notebooks, you can spot drawings of the "ouroborus", a mythical (sea) dragon that would eat its own tail: an ancient representation of self-reference. You see this notion of self-reference emphasized in the theoretical framework of autopoiesis by biologists Humberto Maturana and Francisco Varela, who Wheeler himself took an interest in as evidenced within his notebooks. One also sees notions of life as self-referential subsystems of their environments in the works of Robert Rosen, Stuart Kauffman, Tibor Gánti and others.
But physics is not mere semiotics. We need mathematical formalism. Wheeler was obsessed over 3 decades with Gödel's proof, starting from his initial contact with Gödel at the Institute for Advanced Study in Princeton while completing the famous volume Gravitation written with Charles Misner and Kip Thorne. (Gödel believed quantum theory was not a complete theory, so refused to speak about it.) Wheeler liked to write:
Gödel's Proof: Too important to be left to the mathematicians.
Compare this to the biologist Robert Rosen's landmark Life Itself where he so poetically states:
Clearly the spirit of Gödel can be perceived at this point, hovering nearby.
Wheeler elaborated in his notebook:
ADD "PARTICIPANT" TO "UNDECIDABLE PROPOSITIONS" TO ARRIVE AT PHYSICS
[...] We consider the quantum principle. Of all the well-analyzed features of physics, there is none more central, and none of an origin more mysterious. This note identifies its key idea as participation; and its point of origin, as the "undecidable propositions" of mathematical logic. On the view physics is not machinery. Instead, everything, physics included, derives from two parents, and is nothing but cathode-tube image of the interplay between them. One is the "participant". The other is the complex of undecidable propositions of mathematical logic.
The physicist Karl Svozil also believes there to be a connection, writing:
It is important to distinguish between the "instrinsic' view of an observer, who is entangled with and who is inseparable part of the system, and the "extrinsic" perspective of an observer who is not entangled with the system via self-reference. Indeed the recognition of the importance of intrinsic perception, of a "view from within," might considered as a key observation towards a better understanding of undecidability and complementarity.
Some critics usually do not even engage in speaking about Wheeler, because of the similarity to Penrose's claims about Gödel as fundamental to understanding physics. Penrose's line of reasoning can admittedly be difficult to follow. But dismissing Wheeler's work because of superficial comparisons to Penrose has the same intellectual integrity as arguing that Canada is uninhabitable because Leif Erikson already tried it and famously failed.
More refined arguments will say "not everything that is self-referential is the same" and "not everything that is paradoxical is the same". This is true. But also we can say "not everything that is self-referential is different" and "not everything that is paradoxical is different". It is important to neither accept nor reject after only a superficial glance.
Let's look into the theorem (result) and the proof (the way to get the result). Gödel's theorem states that there are undecidable propositions in Peano arithmetic (arithmetic with + and x ). The proof allows one to list several statements, and make a self-referential statement that is equivalent to "This statement is unprovable". Gödel himself likens this to the ancient liar paradox of Epimenides of Crete.
Gödel's proof and related proofs, such as Turing's proof of the undecidability of the halting problem, rely on self-referential arguments. (Gödel's proof follows from Turing's proof as shown in Turing's famous 1936 paper). We must discuss algorithms before going further. An algorithm is defined in terms of a Turing machine-a mathematical abstraction of a computer with an infinitely long tape- that halts and returns a result. This is called the Church-Turing thesis. An algorithm, among other things, requires consistency, meaning there is no contradiction and demonstrability, as Gödel called it in a postscript to a 1934 lecture, which means that physical symbols can be written down. Demonstrability is the "physical" part of proof --- dots on a screen, chalk on a board, notches on wood. A mathematical proof must require numerals and symbols on a chalkboard, which can be checked mechanically. Now we will see how self-application of Turing machines results in a quasi-paradoxical proof, in a way that may make one think of Penrose's or Escher's staircase.
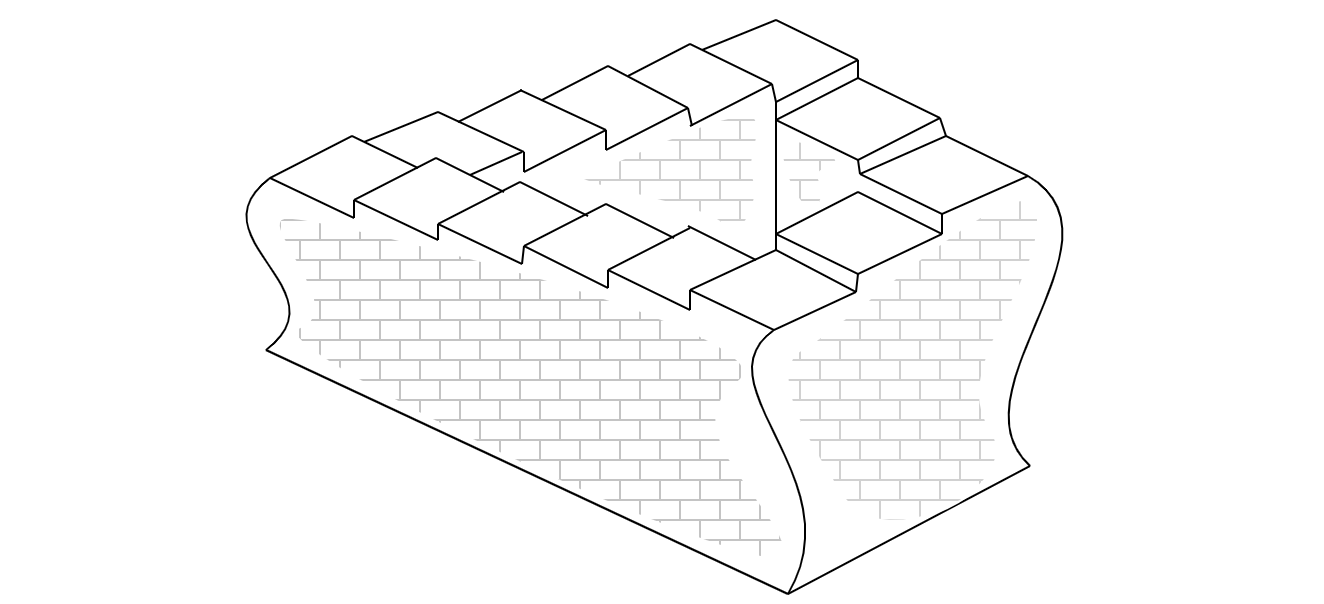
Let's define a universal Turing machine as a Turing machine that can simulate other Turing machines. Now let's say we want to know whether any given Turing machine will run forever or halt and return an answer. This is called the "halting problem". Let's prove, by contradiction, that a generalized algorithm to decide the halting problem cannot exist; it is an undecidable problem. First, imagine a universal Turing machine "H" that will always tell us correctly whether some machine will halt or never halt. Then append to H a negator "N" that runs forever if H detects halting and vice-versa. Put H and N together into a universal Turing machine called X. Now feed X into itself. X halts if and only if X never halts! If there is demonstrability, i.e., provability then there can be no consistency. But if you wish to preserve the mathematical "sacredness" of consistency, one must give up on demonstrability i.e. forfeit provability. Another way of saying this is that we must choose between complete or consistent. Because there is no self-referential algorithm for the halting problem, there can be no generalized algorithm for the halting problem. One single self-referential instance is enough to prove the undecidability of the problem within this formal system. Undecidability proofs act as self-referential subsystem of the general formal system.
How can this be related to the formalism of quantum mechanics? In 1930, John von Neumann identified Process 1 and Process 2 of quantum theory. Process 1, von Neumann described, as a measurement dictated by a probablistic rule called the "Born rule". Process 1 is non-deterministic but demonstrable i.e. physically measurable. Process 2 is deterministic but non-demonstrable (not measurable), describe by the wave function known as Schrödinger's equation. It is consistent every time you run the experiment but you cannot measure the superposed wave function, by definition.
These are commonly called the "Copenhagen rules" or the "shut-up-and-calculate" approach, since there is no interpretation. These are bare-bones raw, unprocessed, unrefined rules. There is also a clear logical inconsistency between Process 1 and Process 2 of the Copenhagen rules. Surely the world only functions by one set of rules, not two juxtaposed rules.
The Many-World Interpretation written by John Wheeler's grad student Hugh Everett III in 1957, aimed to solve this inconsistency, by stating that quantum theory only requires Process 2. Wheeler, in fact, wrote the very first paper in support of it, due to the necessity of describing a quantum system without an external observer in cosmology. Later, Wheeler shifted to his "U-diagram". Today, people defend Everett, citing the powerful tool of decoherence, which in a case of situational irony, contains the very calculations of the Born rule from Process 1, which is what Everett was avoiding, in the diagonal entries of the formalism we call the density matrix. Scott Aaronson claims on his blog Shtetl Optimized that Everett's interpretation is:
clearly and unequivocally the best interpretation of QM that we have,as long as we leave ourselves out of the picture
[emphasis original]
Both Everett's Many World and Wheeler's Gödelian visions of quantum theory contain the consistency that the Copenhagen rules lack, but only one is designed to preserve the notion of measurement as central.
In both Gödel's (and Turing's, etc) proof, one must choose between physical demonstrability (of symbols) and consistency. In the Copenhagen rules, one must choose between physical demonstrability (of measurements) of Process 1 and consistency of Process 2 which we call by the formal name of "unitarity". Now what is meant by "inconsistency"? Does this mean the if an experiment gives a probability of 1/2 for an outcome, that it will change to 1/3 or 1/5 or 2/7? Of course not! The probability distributions in quantum mechanics stay the same. Quantum mechanics is a battle-tested theory.
What is meant in this context is that you can prepare an experiment and measure one outcome. Then you can prepare an experiment precisely the same, then measure a completely different outcome. (This goes beyond classical concept of chaos; flipping a coin yields "random" result because of our ignorance of initial conditions like imperfections in muscle memory, air currents etc).
What is meant by "demonstrable"? In the case of mathematics and theoretical computer science it means a physical symbol; provable. In the case of quantum physics, it means a physically measurable quantity like an audible click from a Geiger counter or a dot appearing on a silver bromide screen from a single photon. Information is fundamental in this picture. As Bohr would say "No elementary phenomena is a phenomenon until it is an observed (or "measured" or "registered") phenomenon".
One might say that undecidability proofs and Copenhagen rules are "isomorphic" or map onto each other, a kind of "Gödel-Bohr" Complementarity. One might also call this Gödel-Quantum isomorophism a Gödel-Quantum "correspondence". (I should note that this specific isomorphism is eisegesis read into, not exegesis read from Wheeler's notebooks, and any mistakes should be attributed to the author).
In this way we can interpret Wheeler's famous dictum "It from Bit" in the light of his unpublished notebooks: "It" means the foundations of science founded on quantum physics and "Bit" means the foundations of theoretical computer science founded on undecidability proofs of Gödel, Tarski, Turing, Rice, Quine, Hartmanis-Stearns and others. The entire Gödel-Quantum correspondence can be summed up in the following phrase:
Demonstrability versus Consistency
Turing also introduced a concept called "oracles". Oracle Turing machines can determine whether or not a Turing machine not equivalent to itself halts similarly to how one can determine the state of a particle not equivalent to itself if entangled.
But do quantum computers negate Wheeler's vision of a Gödelian quantum theory? Do they force us to choose between the computability of quantum computers and uncomputability of Gödel's and Turing's proofs? As the baseball player Yogi Bera would say "When you come to a fork in the road, take it".Assuming a very famous conjecture that feasibly solvable and feasibly verifiable problems are different (experts say P is not equal to NP), then we can divide problems into feasibly decidable, feasibly undecidable and an intermediate class that is feasibly undecided. "Feasible" has a technical definition we will not go into, but for all practical purposes, it just means a short run time compared to the input. Quantum computers can, in general, solve some of the feasibly undecided problems, e.g., factorization, in the intermediate class. Some feasibly undecided problems, like whether a number P is prime or not, were later shown to be feasibly decidable without a quantum algorithm.
This business of quantum computing is delicate. As Scott Aaronson, who has led the crusade against the misunderstanding the quantum computers, are "just trying all solutions in parallel", states in the 2025 Kip Lecture at Harvard:
Quantum computers already look like they are slightly expanding the scope of what mathematical statements we can know.
Quantum computers offer an advantage to classically feasibly "undecided" problems, but not the (conjectured) undecidable problems. Any objection to Wheeler based on quantum computing that states we must choose between quantum or undecidability is a false dichotomy, when we examine the mathematics of quantum computing with a fine-tooth comb.
There have even been questions to unexpected quantum objects and undecidable and uncomputable problems derivable from Godel's proof. For example, Hector Zenil asks
The more information a black hole has, the larger its event horizon, and in no smaller place such information can be contained[....] Black Holes can be regarded thus as perfect data compressors[...] An interesting question in connection to Kolmogorov complexity, given that Kolmogorov complexity is uncomputable, is how nature may have achieved a perfect data compressor, even though its contents and mechanism may have achieved a perfect data compressor, even though its contents and mechanisms may turn out to be inaccessible to us in practice.
What can biological systems have to do with quasars and black holes? Inhospitable regions of the universe certainly have no connection to living beings. We must do some honest accounting, comparing our conceptual credits and debits. Our knowledge of black holes, of quasars, entered into our textbooks by being observed and measured!
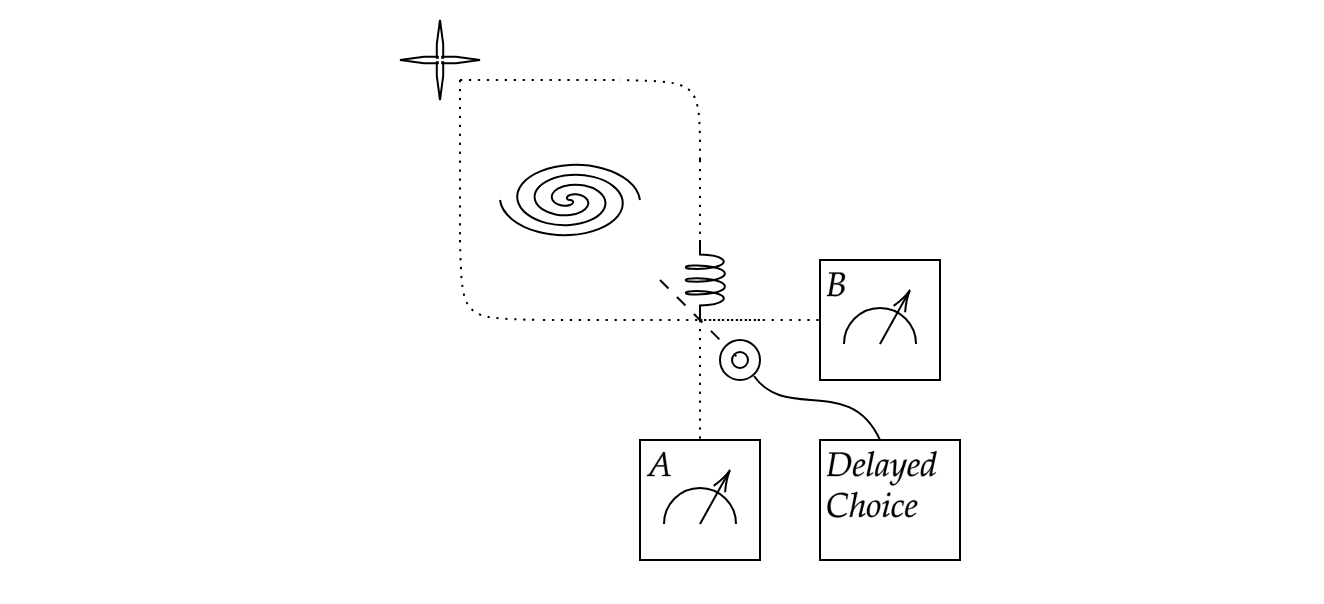
Putting a self-referential subsystem as fundamental to how quantum theory works seems to fly in the face of all common sense. In the first three minutes of the universe, there certainly were an abundance of quantum events, and presumably without any self-referential subsystems, which is the claimed framework for living systems. Are we claiming that there was perhaps some amoeba floating around in the quark-gluon plasma?? No such claim is made here. Then how can a self-referential subsystem be important to quantum processes that precede them by epochs? Enter Wheeler's delayed-choice experiment (not to be confused with the quantum eraser experiment, which relies on different methodologies).
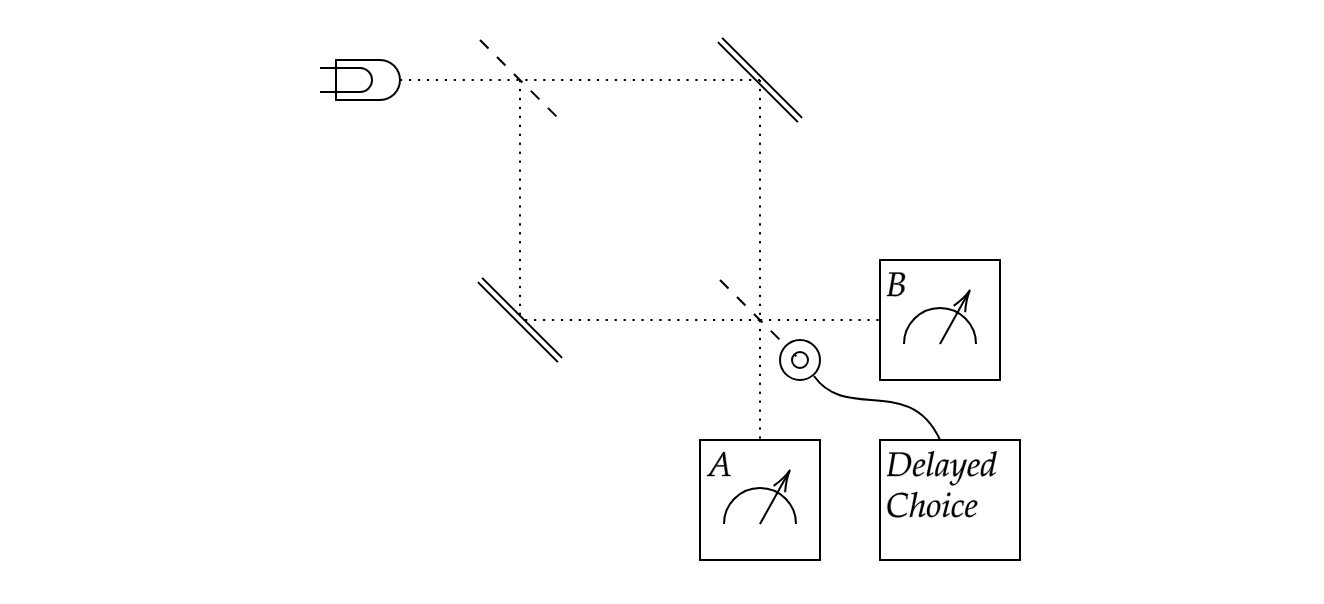
Wheeler asked us to imagine that light is emitted from a star and travels eons through space. Then gravitational lensing by a massive object, like a galaxy cluster, can bend the rays back toward each other. The laws of physics allow a single photon to experience this lensing effect. Then we could have a coiled fiber-optic lens that could delay one side just enough so that the two paths are the same distance. Subsequently, we could put in a half-silvered mirror diagonally between two measurement apparatuses.
If we choose not to put the half-silvered mirror in place, then detector A and detector B will go off in a random way with a 1/2 probability each time. Nothing interesting. However, if we put the half-silvered mirror in place, the two paths have light entering simultaneously, then they will constructively interfere on one side of the half-silvered mirror and destructively interfere, cancelling out any possibility of entering the other detector.
In this way, we can choose, eons after the photon began its journey whether the photon would have taken both paths in a superposed state, making one detector go off 100% of the time, or whether it would have taken a single path, making both detectors go off with a 1/2 probability. We can choose---in principle---whether we would like von Neumann's Process 1 or Process 2 unimaginable epochs after the beginning of the event. (We can choose between consistency or demonstrability long after the experiment began).
We cannot work out this experiment at the moment, but Wheeler also came up with a table-top version of the experiment that has been verified multiple times in multiple different variations of the experiment. Nobel laureate Anton Zeilinger and collaborators have tested and retested this experiment, with success after success.
Not only a spatial subsystem but a temporal subsystem as well.
This illuminates not only the logical foundation of living systems but the chronological origin of living systems as self-referential observation. Those living systems alive now are the ones which were able to go beyond mere self-reference and were able to self-replicate (which implies self-reference).
It is misleading to say consciousness is the foundation for quantum theory. Even Wigner, who is famous for asking this question, acknowledged its shaky ground. Since consciousness is not currently defined in any rigorous fashion, claiming that the battle-tested formalism of quantum mechanics to be based on consciousness is like saying all of science is based on vague feelings. It can lead and has led to a lot of confusion.
Wheeler himself wrestled with the place for consciousness and life within the context of his "U-diagram", and spoke of the "eye" as both as an "observer" and "measuring apparatus". If we clarify that quantum theory is not based on an undefined notion of an "observer", but that the "observer" is defined within this self-referential framework, then we obtain clarity. The observer comes from the quantum, not the quantum from the observer; living systems come from the quantum, not the quantum from living systems. And as Penrose often clarifies: consciousness comes from the quantum, not quantum from consciousness. Gödelian quantum theory provides a framework for living systems in general and consequently for the specific case of whatever "consciousness" one may attribute to neuronal activity. Michael Levin has emphasized that we often overlook non-neuronal intelligence, or more basically information and information processing (and has agreed in a personal correspondence that life, at its core, may be "Gödelian"). We now have a way forward to claim the converse, and saying consciousness is based on Gödelian quantum mechanics.
In this way, Penrose's arguments for a link between Gödel, quantum and "consciousness" can find a footing that do NOT depend on arguments about understanding and cognition. Gödelian consciousness, as defined in terms of neuronal activity, is just a special case of Gödelian living systems.
Discussion
Wheeler noted as we get deeper and deeper we get back to the observer. We cannot talk about black holes and quasars without talking about how we obtained the information about black holes and quasars. Wheeler writes in a 1974 essay with the distinctive Wheelerian title:
"Perspectives: The Universe as Home for Man: Puzzles attached to consciousness, the quantum principle, and how the universe came into being suggest that the greatest discoveries are yet to come":
One view holds that as we keep on investigating matter, we will work down from crystals to molecules, from molecules to atoms, from atoms to particles, from particles to quarks and mine to forever greater depths. A very different concept might be called the "Leibniz logic loop." According to this view the analysis of the physical world, pursued to sufficient depth, will lead back in some now-hidden way to man himself, to conscious mind, tied unexpectedly through the very acts of observation and participation to partnership in the foundation of the universe. To write off the power of observation and reason to make headway with this question would seem to fly against experience.
So we can see how the self-referential subsystem appearing in undecidability proofs of Gödel, Turing and others, the self-referential subsystem of proposed frameworks for living systems by Maturana, Varela, Rosen, Ganti and others, and the self-referential system of John Archibald Wheeler's "observer" in his famous U-diagram, go beyond mere superficial similarities.
In the special issue of Physics Today dedicated to Wheeler (April 2009), Kip Thorne recalls when Richard Feynman heard about this self-referential universe business, the same year that Wheeler took Misner and Thorne along to speak with Gödel. Feynman, like Gödel, was reluctant, but added:
This guy sounds crazy. What people of your generation don’t know is that he has always sounded crazy. But when I was his student, I discovered that if you take one of his crazy ideas and you unwrap the layers of craziness from it one after another like lifting the layers off an onion, at the heart of the idea you will often find a powerful kernel of truth.
In this, it is argued that Wheeler's U-diagram and a formalization with undecidability proofs is precisely what Schrödinger meant by:
"other laws of physics" hitherto unknown
in the quest to answer "What is Life?" As Wheeler liked to say, we are "At home in the Universe".
Davis, Martin. The undecidable: Basic papers on undecidable propositions, unsolvable problems and computable functions. Courier Corporation, 2004.
Ma, Xiao-song, Johannes Kofler, and Anton Zeilinger. "Delayed-choice gedanken experiments and their realizations." Reviews of Modern Physics 88.1 (2016): 015005.
Misner, Charles W., Kip S. Thorne, and John Archibald Wheeler. Gravitation. Macmillan, 1973.
Quine, Willard Van Orman. Mathematical logic. Harvard University Press, 1981.
Rosen, Robert. Life itself: a comprehensive inquiry into the nature, origin, and fabrication of life. Columbia University Press, 1991.
Schrodinger, Erwin. What is life?: With mind and matter and autobiographical sketches. Cambridge university press, 2012.
Wheeler, John A. At home in the universe. 1996.
Wheeler, John Archibald, and Kenneth William Ford. Geons, black holes, and quantum foam: A life in physics. WW Norton & Company, 2000.
Wheeler, John Archibald, and Wojciech Hubert Zurek, eds. Quantum theory and measurement. Princeton University Press, 2014.